Ричард Фейнман - 5. Электричество и магнетизм
- Название:5. Электричество и магнетизм
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 5. Электричество и магнетизм краткое содержание
5. Электричество и магнетизм - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
(3.14)
а для потока из V 2:
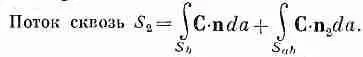
(3.15)
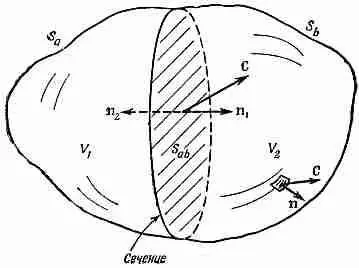
Заметьте, что во втором интеграле мы обозначили внешнюю нормаль к S abбуквой n 1, если она относится к S 1 , и буквой n 2, если она относится к S 1 (см. фиг. 3.4).
Фиг. 3.4. Объем V, заключенный внутри поверхности S, делится на две части «сечением» (поверхностью S ab ). Получается объем V 1 , окруженный поверхностью S 1 = S a +S ab , и объем V 2 , окруженный поверхностью S 2 = S b +S ab .
Ясно, что n 1=-n 2, и тем
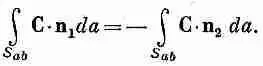
самым
(3.16)
Складывая теперь уравнения (3.14) и (3.15), мы убеждаемся, что сумма потоков сквозь S 1 и S 2 как раз равна сумме двух интегралов, которые, взятые вместе, дают поток через первоначальную поверхность S=S a +S b .
Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V 1 разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначального объема всегда остается справедливым то свойство, что поток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.
§ 3. Поток из куба; теорема Гаусса
Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Dx, ребро куба (а точнее, бруска) в направлении у равно Dy, а в направлении z равно Dz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5).
Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен
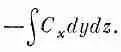
Так как куб считается малым, этот интеграл можно заменить значением С хв центре грани 1 эту точку мы обозначили (1), умноженным на площадь грани DyDz:
Поток сквозь 1 наружу=-C x(1)DyDz.
Подобным же образом поток наружу через грань 2 равен
Поток сквозь 2 наружу= C x(2) DyDz.
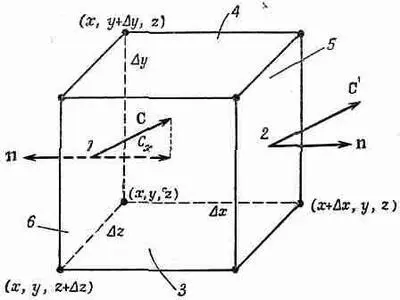
Фиг. 3.5. Вычисление потока вектора С из маленького кубика.
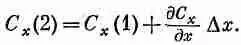
Величины C x (1) и С х (2), вообще говоря, слегка отличаются. Если Dx достаточно мало, то можно написать
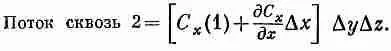
Существуют, конечно, и другие члены, но в них входит (Dx) 2и высшие степени Dx, и в пределе малых Dx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
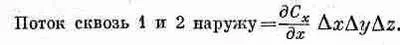
Складывая потоки через грани 1 и 2, получаем
Производную нужно вычислять в центре грани 1, т. е. в точке [x,y+(Dy/2), z+(Dz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).
Повторяя те же рассуждения с каждой парой граней, мы получаем
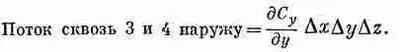
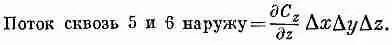
а
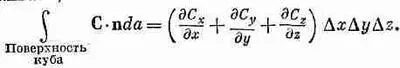
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
Сумма производных в скобках как раз есть С·С, a DxDyDz=DV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
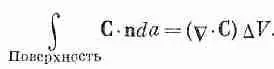
(3.17)
Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р. Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.
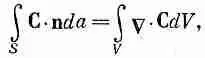
ТЕОРЕМА ГАУССА
(3.18)
где S — произвольная замкнутая поверхность, V — объем внутри нее.
§ 4, Теплопроводность; уравнение диффузии
Чтобы привыкнуть к теореме, разберем на примере, как ее применяют. Обратимся опять к распространению тепла, скажем в металле, рассмотрим совсем простой случай: все тепло было подведено к телу заранее, а теперь тело остывает. Источников тепла нет, так что количество тепла сохраняется. Сколько же тогда тепла должно оказаться внутри некоего определенного объема в какой-то момент времени? Оно должно уменьшаться как раз на то количество, которое уходит с поверхности объема. Если этот объем — маленький кубик, то,
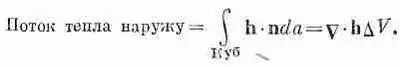
следуя формуле (3.17), можно написать
(3.19)
Но это должно быть равно скорости потери тепла внутренностью куба. Если q — количество тепла в единице объема, то весь
запас тепла в кубе qDV, а скорость потерь равна
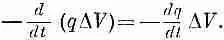
Интервал:
Закладка:





