Ричард Фейнман - 5. Электричество и магнетизм
- Название:5. Электричество и магнетизм
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 5. Электричество и магнетизм краткое содержание
5. Электричество и магнетизм - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
(Сш)X(Сj)№0 (в общем случае).
К счастью, к таким выражениям мы прибегать не будем. (Но сказанное нами не меняет того факта, что СjXСm =0 в любом скалярном поле: здесь обе Сдействуют на одну и ту же функцию.) Подвох номер два (он тоже в нашем курсе не встретится): правила, которые мы здесь наметили, выглядят просто и красиво только в прямоугольных координатах. Например, если мы хотим написать x-компоненту выражения С 2h, то сразу пишем
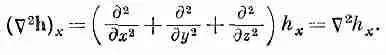
(2.60)
Ио это выражение не годится, если мы ищем радиальную компоненту С 2h. Она не равна С 2h r. Дело в том, что в алгебре векторов все их направления полностью определены. А когда мы имеем дело с векторными полями, то их направления в разных местах различны. Когда мы пробуем описать векторное поле, например, в полярных координатах, то «радиальное» направление меняется от точки к точке. И начав дифференцировать компоненты, вы запросто можете попасть в беду. Даже в постоянном векторном поле радиальная компонента от точки к точке меняется.
Обычно безопаснее и проще всего держаться прямоугольных координат. Но стоит упомянуть и одно исключение: поскольку лапласиан С 2есть скаляр, то можно писать его в любой системе координат (скажем, в полярных координатах). Но так как это дифференциальный оператор, то применять его надо только к векторам с фиксированным направлением компонент, т. е. к заданным в прямоугольных координатах. Итак, расписывая наши векторные дифференциальные уравнения покомпонентно, мы будем предварительно выражать все наши векторные поля через их х-, у-, z-компоненты.
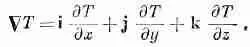
* В наших обозначениях выражение (а, b, с) представляет вектор с компонентами а, b, с. Если вам нравится пользоваться единичными векторами i, j и k, то можно написать
* Мы рассматриваем h как физическую величину, зависящую от положения в пространстве, а не как заданную математически функцию трех переменных. Когда h «дифференцируется» по х, у и z или по х', у' и z', то математическое выражение для h должно быть предварительно выражено в виде функции соответствующих переменных, Поэтому в новой системе координат мы не отмечаем h штрихом.
Глава 3
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ
§1.Векторные интегралы; криволинейный интеграл от ▽ш
§2.Поток векторного поля
§З. Поток из куба; теорема Гаусса
§4.Теплопроводность; уравнение диффузии
§5.Циркуляция векторного поля
§6. Циркуляция по квадрату; теорема Стокса
§7. Поля без роторов и поля без дивергенций
§8.Итоги
§ 1. Векторные интегралы;
криволинейный интеграл от Сш
В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено довольно много, все их можно подытожить одним правилом: операторы д/дх, д/ду и д/dz суть три компоненты векторного оператора у. Сейчас нам хотелось бы лучше разобраться в значении производных поля. Тогда мы легче почувствуем смысл векторных уравнений поля.
Мы уже говорили о смысле операции градиента (С на скаляр). Обратимся теперь к смыслу операций вычисления дивергенции (расходимости) и ротора (вихря). Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Но уравнения эти, к несчастью, нельзя вывести из векторной алгебры при помощи каких-либо легких подстановок, так что вам придется учить их как что-то новое. Одна из этих интегральных формул практически тривиальна, а другие две — нет. Мы выведем их и поясним их смысл. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при разработке общих физических теорий. Для теории полей эти математические теоремы — все равно, что теорема о сохранении энергии для механики частиц. Подобные теоремы общего характера очень важны для более глубокого понимания физики. Но вы увидите, что, за немногими простыми исключениями, они мало что дают для решения задач. К счастью, как
раз в начале нашего курса многие простые задачи будут решаться именно этими тремя интегральными формулами.
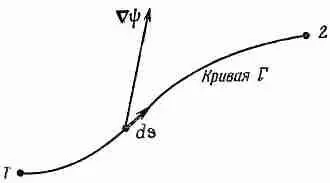
Фиг. 3.1. Иллюстрация уравнения (3.1).
Вектор Сш вычисляется на линейном элементе ds.
Позже, однако, когда задачи станут потруднее, этими простыми методами мы больше обойтись не сможем.
Мы начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ш (x, у, z). В двух произвольных точках (1) и (2) функция я|з имеет соответственно значения ш(l) и ш(2). [Используется такое удобное обозначение: (2) означает точку (x 2, y 2, z 2), а ш(2) это то же самое, что ш(x 2, y 2, z 2).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива
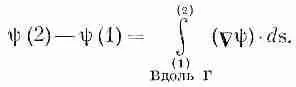
Т Е О Р Е М А 1
(3.1)
Интеграл, стоящий здесь, это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора Сш) на другой вектор, ds, являющийся бесконечно малым элементом дуги кривой Г [направленной от (1) к (2)].
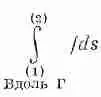
Напомним, что мы понимаем под криволинейным интегралом. Рассмотрим скалярную функцию f(x, y, z) и кривую Г, соединяющую две точки (1) и (2). Отметим на кривой множество точек и соединим их хордами, как на фиг. 3.2. Длина i-й хорды равна Ds i,-, где i пробегает значения 1, 2, 3, .... Под криволинейным интегралом
подразумевается предел суммы

где f i— значение функции где-то на i-й хорде. Предел — это то,
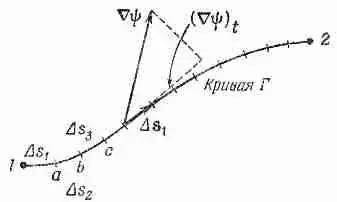
Фиг. 3.2. Криволинейный интеграл есть предел суммы.
к чему стремится сумма, когда растет число хорд (разумным образом, чтобы даже наибольшее Ds i®0).
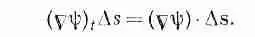
Интервал:
Закладка:





