Ричард Фейнман - 5. Электричество и магнетизм

Т 1= Т(х, у, z) и Т 2=Т(х + Dx, у + Dу, z + Dz),

где Dx:, Dy, Dz — компоненты вектора DR(фиг. 2.5). Вспомнив (2.7), напишем

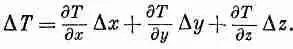
(2.13)

Слева в (2.13) стоит скаляр, а справа — сумма трех произведе­ний каких-то чисел на Dx;, Dy, Dz, которые являются компонен­тами вектора. Значит,

три числа — тоже х-, у- и z-компоненты вектора.

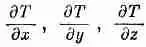
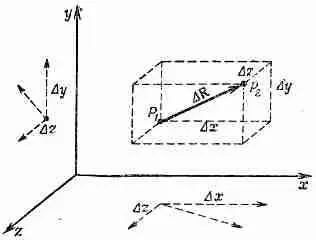
Фиг. 2.5. Вектор DR с компо­нентами Dx, Dу, Dz.

Мы напишем этот новый вектор при помощи символа С Т. Символ С (называемый набла) — это D вверх ногами; он напоминает нам о дифференцировании. Читают С T по-разному:

«набла T», или «градиент T», или «gradT»:

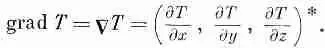
(2.14)

С этим обозначением (2.13) переписывается в более компакт­ной форме

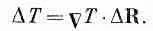
(2.15)

Или, выражая словами: разница температур в двух близких точках есть скалярное произведение градиента Т на вектор смещения второй точки относительно первой. Форма (2.15) так­же служит иллюстрацией к нашему утверждению, что ДТ — действительно вектор.

Быть может, вы еще не убеждены? Тогда докажем иначе. (Хотя, вглядевшись внимательно, вы увидите, что это на самом деле то же самое доказательство, только подлиннее!) Мы по­кажем, что компоненты ДТ преобразуются абсолютно так же, как я компоненты R, а значит, ДТ — тоже вектор в соответствии с первоначальным определением вектора в вып. 1, гл. 11. Мы выберем новую систему координат х', у', z' и в ней вычис­лим дТ/дх', дТ/ду' : дТ/dz'. Для простоты положим z=z', так что о третьей координате мы можем позабыть. (Можете сами заняться проверкой более общего случая.)

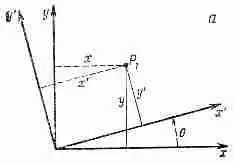
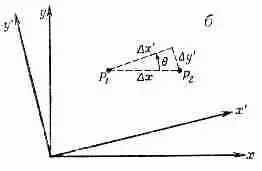
Фиг. 2.6. Переход к повернутой системе координат (а) и частный

случай интервала DR , параллель­ного к оси х (б).

Выберем систему х', у', повернутую относительно х, y-системы на угол 9 (фиг. 2.6, а). Координаты точки (х, у) в штрихованной системе имеют вид:

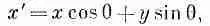
(2.16)

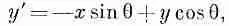
(2.17)

или, решая относительно x и y,

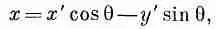
(2.18)

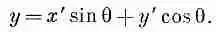
(2.19)

Если всякая пара чисел преобразуется так же, как x и y, то она является компонентами вектора.

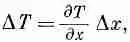
Рассмотрим теперь разницу в температурах двух сосед­них точек Р 1 и Р 2 (фиг. 2.6, б). В координатах х, у запишем

(2.20)

так как Dy = 0.

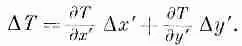
А в штрихованной системе? Там мы бы написали

(2.21)

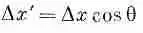
Глядя на фиг. 2.6, б, мы видим, что

(2.22)

и

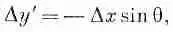
(2.23)

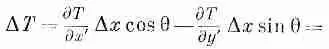
так как Dy отрицательно при положительном Dx. Подстав­ляя в (2.21), получаем

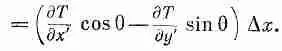
(2.24)

(2.25)

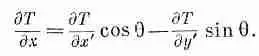
Сравнивая (2.25) с (2.20), мы видим, что

(2.26)

Это уравнение говорит нам, что дТ/дх получается из дТ/дх' и дТ/ду' в точности так же, как х из х' и у' в (2.18). Значит, дТ/дх — это x-компонента вектора. Сходные же рассуждения показывают, что дТ/ду и dT/dz суть у- и z-компоненты. Стало быть, СТ есть на самом деле вектор. Это векторное поле, обра­зованное из скалярного поля Т.

§ 4. Оператор С

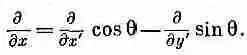
А сейчас мы проделаем крайне занятную и остроумную вещь — одну из тех, которые так украшают математику. До­казательство того, что grad Т, или С T является вектором, не зависит от того, какое скалярное поле мы дифференцируем. Все доводы остались бы в силе, если бы Т было заменено любым скалярным полем. А поскольку уравнения преобразований одинаковы независимо от того, что дифференцируется, то можно Т убрать и уравнение (2.26) заменить операторным уравнением

(2.27)

Как выразился Джинс, мы оставляем операторы «жаждущими продифференцировать что угодно».

Так как сами дифференциальные операторы преобразуются как компоненты векторного поля, то можно назвать их компо­нентами векторного оператора. Можно написать

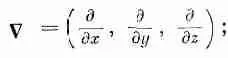
(2.28)

это означает, конечно,

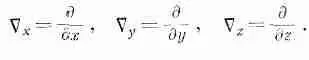
(2.29)

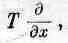
Мы абстрагировали градиент от Т — в этом и есть остроумие. Конечно, вы должны все время помнить, что С — это опе­ратор. Сам по себе он ничего не означает. А если С сам по себе ничего не означает, то что выйдет, если мы градиент помножим на скаляр, например на T, чтобы получилось произведе­ние TС? (Ведь вектор всегда можно умножить на скаляр.) Это опять ничего не означает. Компонента х этого выражения равна

(2.30)

а это не число, а все еще какой-то оператор. Однако в согласии с алгеброй векторов Т Спо-прежнему можно называть векто­ром.

А сейчас помножим С на скаляр с другой стороны. Полу­чится произведение С T. В обычной алгебре

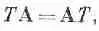
(2.31)

но нужно помнить, что операторная алгебра немного отличается от обычной векторной. Надо всегда выдерживать правильный порядок операторов, чтобы их операции имели смысл. Тогда у вас трудностей не возникнет, если вы припомните, что опе­ратор y подчиняется тем же условиям, что и производные. То, что вы дифференцируете, должно быть поставлено справа от С Порядок здесь существен.