Ричард Фейнман - 5. Электричество и магнетизм

В нашей теореме (3.1) интеграл означает то же самое, хоть и выглядит чуть по-иному. Вместо f стоит другой скаляр — составляющая Сш в направлении Ds. Если обозначить эту составляющую через (Сш) t , то ясно, что

(3.2)

Интеграл в (3.1) и подразумевает сумму таких членов.

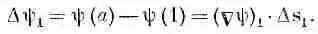
А теперь посмотрим, почему уравнение (3.1) правильно. В гл. 1 мы показали, что составляющая Сш вдоль малого сме­щения DR равна быстроте изменения ш в направлении DR. Рассмотрим хорду кривой Ds от точки (1) до точки а на фиг. 3.2. По нашему определению

(3.3)

Точно так же мы имеем

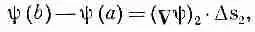
(3.4)

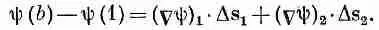
где, конечно, (Сш) 1означает градиент, вычисленный на хорде Ds 1, a (Сш) 2— градиент, вычисленный на Ds 2. Сложив (3.3) и (3.4), получим

(3.5)

Вы видите, что, продолжая прибавлять такие члены, мы полу­чаем в итоге

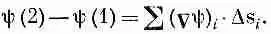
(3.6)

Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как ра­венство не зависит и от выбора точек а, b, с,..., точно так же оно не зависит от выбора самой кривой Г. Теорема верна для любой кривой, соединяющей точки (1) и (2).

Два слова об обозначениях. Не будет путаницы, если писать для удобства

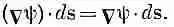
(3.7)

Тогда наша теорема примет такой вид:

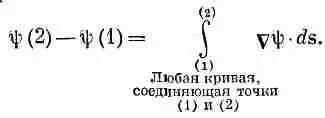
Т Е О Р Е М А 1

(3.8)

§ 2. Поток векторного поля

Прежде чем рассматривать следующую интегральную теоре­му — теорему о дивергенции,— хотелось бы разобраться в од­ной идее, смысл которой в случае теплового потока легко усваи­вается. Мы уже определили вектор h, представляющий коли­чество тепла, протекающего сквозь единицу площади в еди­ницу времени. Положим, что внутри тела имеется замкнутая поверхность S, ограничивающая объем V (фиг. 3.3). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S.

Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху, то

da = dxdy.

Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого куби­ка и обозначать его dV, подразумевая, что

dV= dxdydz.

Кое-кто пишет и d 2 a вместо da, чтобы напомнить самому себе, что это выражение второй степени; вместо dV пишут также d 3V. Мы будем пользоваться более простыми обозначениями, а вы уж постарайтесь не забывать, что у площадей бывают два измерения, у объемов — три.

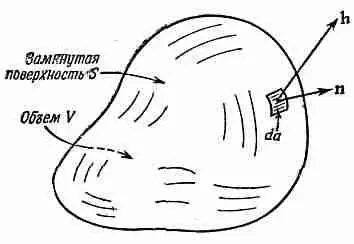
Фиг. 3.3. Замкнутая поверх­ность S, ограничивающая объем V.

Единичный вектор n — внешняя нор­маль к элементу поверхности da, a h — вектор теплового потопа сквозь элемент поверхности.

Поток тепла через элемент поверхности da равен произведе­нию площади на составляющую h, перпендикулярную к da. Мы уже определяли n — единичный вектор, направленный наружу перпендикулярно к поверхности (см. фиг. 3.3). Искомая составляющая h равна

h n=h·n, (3.9)

и тогда поток тепла сквозь da равен

h · nda. (3.10)

А весь поток тепла через произвольную поверхность получается суммированием вкладов от всех элементов поверхности. Иными словами, (3.10) интегрируется по всей поверхности

(3.11)

Этот интеграл мы будем называть «поток hчерез поверх­ность». Мы рассматриваем hкак «плотность потока» тепла, а поверхностный интеграл от h— это общий поток тепла наружу через поверхность, т. е. тепловая энергия за единицу времени (джоули в секунду).

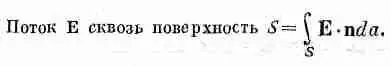
Мы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормаль­ную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем упот­реблять слово

«поток». Мы будем говорить, что

(3.12)

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же опре­деление будет применяться и тогда, когда поверхность незамк­нута.

А возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется. Представьте себе, к примеру, материал, в котором после перво­начального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой по­верхности наружу поступает тепло, содержание тепла во внут­реннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

(3.13)

где Q — запас тепла внутри S. Поток тепла из S наружу равен со знаком минус быстроте изменения со временем общего за­паса тепла Q внутри S. Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

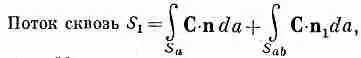
Укажем теперь на интересное свойство потока любого век­тора. Можете при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представьте себе замкнутую поверхность S, окружающую объем V. Разобьем теперь объем на две части каким-то «сече­нием» (фиг. 3.4). Получились два объема и две замкнутые по­верхности. Объем V 1окружен поверхностью S 1 , составленной частью из прежней поверхности S aи частью из «сечения» S ab . Объем V 2окружен поверхностью S 2, составленной из остатка прежней поверхности ( S b ) и замкнутой сечением S ab . Зададим вопрос: если мы рассчитаем поток через поверхность S lи при­бавим к нему поток сквозь поверхность S 2, будет ли их сумма равна потоку через первоначальную поверхность? Ответ гласит: «Да». Потоки через часть S ab , общую обеим поверхностям S 1 и S 2, в точности сократятся. Для потока вектора С из V 1 можно написать