Ричард Фейнман - 5. Электричество и магнетизм

Ну а как насчет плавных траекторий? Получим ли мы тот же ответ? Этот вопрос мы обсудили в вып. 1, гл. 13. Пользуясь теми же доводами, что и тогда, мы можем заключить, что работа переноса единичного заряда от а до b от пути не зависит:

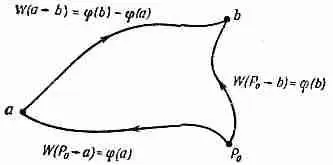
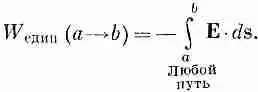
Фиг. 4.4. Работа, затрачен­ная на движение вдоль любого пути от а до b, равна минус работе от некоторой точки Р 0 до а плюс работа от Р 0 до b.

А раз выполняемая работа зависит только от концов пути, то она может быть представлена в виде разности двух чисел. В этом можно убедиться следующим образом. Выберем отправ­ную точку Р 0 и договоримся оценивать наш интеграл, пользуясь только теми траекториями, которые проходят через точку Р 0 . Обозначим работу, выполненную при движении против поля от Р 0 до точки а, через j(а), а работу на участке от Р 0 до точки b — через j(b) (фиг. 4.4). Работа перехода от а к Р 0 (по дороге к b ) равна j (a) с минусом, так что

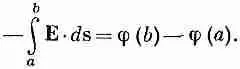
(4.21)

Так как повсюду будет встречаться только разность значе­ний функции j в двух точках, то положение точки Р 0 в сущности безразлично. Однако как только отправная точка выбрана, число j тем самым определяется в любой точке пространства; значит, j является скалярным полем, функцией от х, у, z. Эту скалярную функцию мы называем электростатическим потен­циалом в произвольной точке.

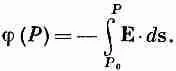
Электростатический потенциал

(4.22)

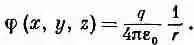
Часто очень удобно брать отправную точку на бесконеч­ности. Тогда потенциал j одиночного заряда в начале коорди­нат, взятый в произвольной точке (х, у, z), равен [см. уравнение (4.20)]

(4.23)

Электрическое поле нескольких зарядов можно записать в виде суммы электрических полей от первого заряда, от вто­рого, от третьего и т. д. Интегрируя сумму для того, чтобы определить потенциал, мы придем к сумме интегралов. Каждый из них — это потенциал соответствующего заряда. Значит, по­тенциал j множества зарядов есть сумма потенциалов каждого из зарядов по отдельности. Таким образом, и для потенциалов существует принцип наложения. Пользуясь такими же аргу­ментами, как и тогда, когда мы искали электрическое поле группы зарядов или распределения зарядов, мы можем полу­чить окончательные формулы для потенциала j в точке, обозна­ченной как (1):

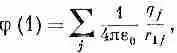
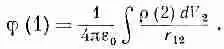
(4.24)

(4.25)

Не забывайте, что потенциал j имеет физический смысл: это потенциальная энергия, которую имел бы единичный заряд, если его перенести в указанную точку пространства из неко­торой отправной точки.

§4. E = -Сj

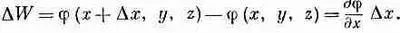
С какой стати нас заинтересовал потенциал j? Силы, дейст­вующие на заряды, даются величиной Е — электрическим полем. Вся соль в том, что Е из j очень легко получить, не труд­нее, чем вычислить производную. Рассмотрим две точки с одина­ковыми у и z, но с разными х: у одной х, у другой x+Dx;; поинте­ресуемся, какую работу надо совершить, чтобы перенести еди­ничный заряд из одной точки в другую. Путь переноса — го­ризонтальная линия от хдо х+Dx.Работа равна разности по­тенциалов в двух точках

Но работа против действия силы на том же отрезке равна

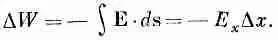
Мы видим, что

(4.26)

Равным образом, Е у =-дj/ду, E z =-dj/dz; все это в обозна­чениях векторного анализа можно подытожить так:

4.27)

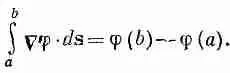
Это дифференциальная форма уравнения (4.22). Любую задачу, в которой заряды заданы, можно решить, вычислив по (4.24) или (4.25) потенциал и рассчитав по (4.27) поле. Уравнение (4.27) согласуется также с тем, что получается в векторном ана­лизе: с тем, что для любого скалярного поля

(4.28)

Согласно уравнению (4.25), скалярный потенциал j пред­ставляется трехмерным интегралом, подобным тому, кото­рый мы писали для Е. Есть ли какая выгода в том, что вместо Е вычисляется j? Да. Для вычисления j нужно взять один ин­теграл, а для вычисления Е—три (ведь это вектор). Кроме того, обычно 1/r интегрировать легче, чем x/r 3. Во многих прак­тических случаях оказывается, что для получения электриче­ского поля легче сперва подсчитать j, а после взять градиент, чем вычислять три интеграла для Е. Это просто вопрос удобства.

Но потенциал j имеет и глубокий физический смысл. Мы показали, что Е закона Кулона получается из Е=-gradj, где j дается уравнением (4.22). Но если Е—это градиент скаляр­ного поля, то, как известно из векторного исчисления, ротор Е должен обратиться в нуль:

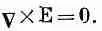
(4.29)

Но это и есть наше второе основное уравнение электростатики — уравнение (4.6). Таким образом, мы показали, что закон Кулона дает поле Е, удовлетворяющее этому условию. Так что до сих пор все в порядке.

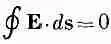
На самом деле то, что СXЕ равно нулю, было доказано еще до того, как мы определили потенциал. Мы показали, что ра­бота обхода по замкнутому пути равна нулю, т. е. по любому пути.

Мы видели в гл. 3, что в таком поле СXЕ должно быть всюду равно нулю. Электрическое поле электро­статики — это поле без роторов.

Вы можете потренироваться в векторном исчислении, дока­зав равенство нулю вектора СXЕ другим способом, т. е. вычис­лив компоненты вектора СXЕ для поля точечного заряда по формулам (4.11). Если получится нуль, то принцип наложения обеспечит нам обращение СXЕ в нуль для любого распределе­ния зарядов.