Ричард Фейнман - 5. Электричество и магнетизм

где e 0— некоторая постоянная (читается эпсилон-нуль). Если внутри поверхности нет зарядов, а вне ее (даже совсем рядом) есть, то все равно средняя нормальная компонента Е равна нулю, так что никакого потока через поверхность нет. Чтобы показать пользу от такого типа утверждений, мы дока­жем, что уравнение (1.6) совпадает с законом Кулона, если только учесть, что поле отдельного заряда обязано быть сфери­чески симметричным. Проведем вокруг точечного заряда сферу. Тогда средняя нормальная компонента в точности равна значе­нию Е в любой точке, потому что поле должно быть направлено по радиусу и иметь одну и ту же величину во всех точках сферы. Тогда наше правило утверждает, что поле на поверхности сферы, умноженное на площадь сферы (т. е. вытекающий из сферы поток), пропорционально заряду внутри нее. Если увеличивать радиус сферы, то ее площадь растет, как квадрат радиуса. Произведение средней нормальной компоненты электрического поля на эту площадь должно по-прежнему быть равно внутрен­нему заряду, значит, поле должно убывать, как квадрат рас­стояния; так получается поле «обратных квадратов».

Если взять в пространстве произвольную кривую и измерить циркуляцию электрического поля вдоль этой кривой, то ока­жется, что она в общем случае не равна нулю (хотя в кулоновом поле это так). Вместо этого для электричества справедлив вто­рой закон, утверждающий, что

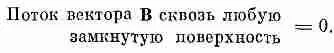
И, наконец, формулировка законов электромагнитного поля будет закончена, если написать два соответствующих уравнения для магнитного поля В:

(1.8)

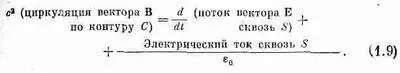
А для поверхности S, ограниченной кривой С:

Появившаяся в уравнении (1.9) постоянная с 2— это квадрат скорости света. Ее появление оправдано тем, что магнетизм по существу есть релятивистское проявление электричества. А константа e опоставлена для того, чтобы возникли привычные единицы силы электрического тока.

Уравнения (1.6) — (1.9), а также уравнение (1.1) — это все законы электродинамики.

Как вы помните, законы Нью­тона написать было очень просто, но из них зато вытекало мно­жество сложных следствий, так что понадобилось немало времени, чтобы изучить их все. Законы электромагнетизма написать несравненно трудней, и мы должны ожидать, что следствия из них будут намного более запутаны, и теперь нам придется очень долго в них разбираться.

Мы можем проиллюстрировать некоторые законы электро­динамики серией несложных опытов, которые смогут нам пока­зать хотя бы качественно взаимоотношения электрического и магнитного полей. С первым членом в уравнении (1.1) вы зна­комитесь, расчесывая себе волосы, так что о нем мы говорить не будем. Второй член в уравнении (1.1) можно продемонстриро­вать, пропустив ток по проволоке, висящей над магнитным бруском, как показано на фиг. 1.6. При включении тока про­волока сдвигается из-за того, что на нее действует сила F=qvXB. Когда по проводу идет ток, заряды внутри него движутся, т. е. имеют скорость v, и на них действует магнит­ное поле магнита, в результате чего провод отходит в сторону.

Когда провод сдвигается влево, можно ожидать, что сам магнит испытает толчок вправо. (Иначе все это устройство можно было бы водрузить на платформу и получить реактивную систему, в которой импульс не сохранялся бы!) Хотя сила чересчур мала, чтобы можно было заметить движение магнитной палочки, однако движение более чувствительного устройства, скажем стрелки компаса, вполне заметно.

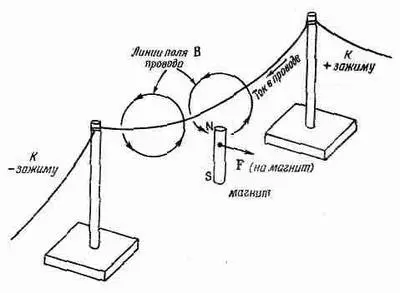
Каким же образом ток в проводе толкает магнит? Ток, теку­щий по проводу, создает вокруг него свое собственное магнит­ное поле, которое и действует на магнит. В соответствии с по­следним членом в уравнении (1.9) ток должен приводить к цир­куляции вектора В; в нашем случае линии поля В замкнуты вокруг провода, как показано на фиг. 1.7. Именно это поле В и ответственно за силу, действующую на магнит.

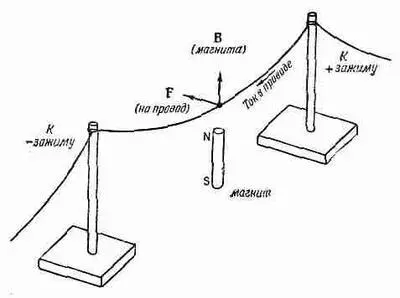
Фиг. 1.6. Магнитная палочка, создающая возле провода поле В.

Когда по проводу идет ток, провод смещается из-за действия силы F = q vXB.

Уравнение (1.9) сообщает нам, что при данной величине тока, текущего по проводу, циркуляция поля В одинакова для любой кривой, окружающей провод. У тех кривых (окружно­стей, например), которые лежат далеко от провода, длина ока­зывается больше, так что касательная компонента В должна убывать. Вы видите, что следует ожидать линейного убывания В с удалением от длинного прямого провода.

Мы сказали, что ток, текущий по проводу, образует вокруг него магнитное поле и что если имеется магнитное поле, то оно действует с некоторой силой на провод, по которому идет ток.

Фиг. 1.7. Магнитное поле тока, текущего по про­воду, действует на магнит с некоторой силой.

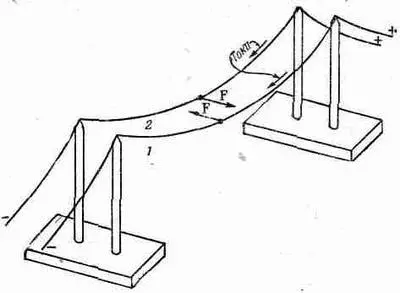
Фиг. 1.8. Два провода, по которым течет ток,

тоже действуют друг на друга с определенной силой.

Значит, следует думать, что если магнитное поле будет создано током, текущим в одном проводе, то оно будет действовать с не­которой силой и на другой провод, по которому тоже идет ток. Это можно показать, применив два свободно подвешенных про­вода (фиг. 1.8). Когда направление токов одинаково, провода притягиваются, а когда направления противоположны — от­талкиваются.

Короче говоря, электрические токи, как и магниты, создают магнитные поля. Но тогда что же такое магнит? Раз магнитные поля создаются движущимися зарядами, то не может ли ока­заться, что магнитное поле, созданное куском железа, на самом деле есть результат действия токов? Видимо, так оно и есть. В наших опытах можно заменить магнитную палочку катушкой с навитой проволокой, как показано на фиг. 1.9. Когда ток проходит по катушке (как и по прямому проводу над нею), наблюдается точно такое же движение проводника, как и преж­де, когда вместо катушки стоял магнит. Все выглядит так, как если бы внутри куска железа непрерывно циркулировал ток. Действительно, свойства магнитов можно понять как непре­рывный ток внутри атомов железа. Сила, действующая на маг­нит на фиг. 1.7, объясняется вторым членом в уравнении (1.1).