Ричард Фейнман - 4. Кинетика. Теплота. Звук

Два закона термодинамики часто формулируют так:

Первый закон: Энергия Вселенной всегда постоянна. Второй закон: Энтропия Вселенной всегда возрастает.

Это не слишком хорошая формулировка второго закона. В ней ничего не говорится, например, о том, что энтропия не из­меняется после обратимого цикла и не уточняется само понятие энтропии. Просто это легко запоминаемая форма обоих законов, но из нее нелегко понять, о чем собственно идет речь.

Все законы, о которых сейчас шла речь, мы собрали в табл. 44.1. А в следующей главе мы используем эту сводку за­конов, чтобы найти соотношение между теплом, выделяемым резиной при растяжении, и дополнительным натяжением рези­ны при ее нагревании.

Таблица 44. 1 · ЗАКОНЫ ТЕРМОДИНАМИКИ

* Раньше мы определяли температурную шкалу иначе. Мы утверждали, что средняя кинетическая энергия молекулы идеального газа пропорциональна температуре или, согласно закону идеального газа, что pV пропорционально Т. Эквивалентно ли это новому определению? Да. Ведь окончательный результат (44.7), выведенный из закона идеаль­ного газа, совпадает с приведенным здесь результатом. Мы еще поговорим об этом в следующей главе.

§ 1. Внутренняя энергия

§ 2. Применения

§ 3. Уравнение Клаузиуса –Клайперона

§ 1. Внутренняя энергия

Когда приходится использовать термоди­намику для дела, то оказывается, что она очень трудный и сложный предмет. В этой книге, однако, мы не будем залезать в самые дебри. Эта область особенно интересна для химиков и инженеров, и тем, кому захочется получше познакомиться с ней, следует обратиться к физи­ческой химии или инженерной термодинамике. Есть еще ряд хороших справочных книг, в кото­рых эта тема обсуждается более подробно.

Термодинамика сложна потому, что каждое явление она позволяет описывать многими способами. Если нам нужно описать поведение газа, то мы можем исходить из того, что его давление зависит от температуры и объема, а можно предположить, что объем зависит от давления и температуры. То же самое и с внутренней энергией U: можно сказать, что она определяется температурой и объемом, стоит только выбрать именно эти переменные, но можно говорить о зависимости от температуры и давления или от давления и объема и т. д. В предыдущей главе мы познакомились с дру­гой функцией температуры и объема, называе­мой энтропией S. И теперь ничто не помешает нам построить другие функции этих переменных. Например, функция U-TS тоже зависит от температуры и объема. Таким образом, нам при­ходится иметь дело с большим количеством разных величин, зависящих от разнообразных комбинаций переменных.

Чтобы упростить понимание этой главы, договоримся с самого начала выбрать в качестве независимых переменных температуру и объ­ем. Химики используют для этого температуру и давление, потому что их легче измерять и контролиро­вать в химических реакциях. Но мы используем повсюду в этой главе температуру и объем и изменим этому только в одном месте, чтобы посмотреть, как совершается переход к химическим переменным.

Итак, сначала рассмотрим только одну систему независимых переменных — температуру и объем. Затем нас будут интере­совать только две функции этих переменных: внутренняя энер­гия и давление. Все другие термодинамические функции можно получить с помощью этих двух, но не обязательно это делать именно сейчас. Даже после таких ограничений термодинамика останется еще трудным предметом, но все же уже не столь невоз­можным для понимания!

Сначала немного займемся математикой. Если величина есть функция от двух переменных, то дифференцировать ее придется осторожнее, чем мы это делали раньше, имея дело с одной пере­менной. Что мы понимаем под производной давления по темпе­ратуре? Изменение давления, сопровождающее изменение тем­пературы, разумеется, зависит от того, что случилось с объемом, пока менялась температура. Прежде чем понятие производной по температуре обретет ясный смысл, надо сказать что-то опре­деленное об изменении объема. Например, можно спросить, какова скорость изменения Р относительно Т при постоянном объеме. Тогда отношение изменений обеих этих величин, по существу, обычная производная, которой привыкли присваи­вать символ dP/dT. Мы обычно используем особый символ дР/дТ, он напоминает нам, что Р зависит, кроме Т, еще и от переменной V, и эта переменная не изменяется. Чтобы подчерк­нуть тот факт, что V не изменяется, мы не только используем символ д, но еще пометим индексом остающуюся постоянной переменную (дР/дТ) у . Конечно, поскольку имеются только две независимые переменные, то это обозначение излишне, но оно, быть может, поможет нам легче пройти сквозь термодинамиче­ские дебри частных производных.

Предположим, что функция f(x, у) зависит от двух незави­симых переменных х и у. Под символом (дf/дх) у мы понимаем самую обычную производную, получаемую общепринятым спо­собом, если у постоянна:

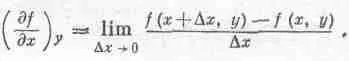
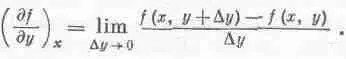
Аналогично определяется и

Например, если f(x, у)=х 2 +ух, то (df/dx) y =2x+y, а (дfду) х =х. Мы можем распространить это на старшие производные:

д 2 f/дy 2 или д 2 f/дудх.

Последний случай означает, что сначала f продифференцировано по х, считая у постоянным, а затем ре­зультат продифференцирован по у, но теперь постоянным стало х. Порядок дифференцирования не имеет значения:

д 2 fldxdy=д 2 f/дyдx.

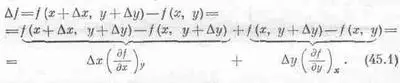
Нам придется подсчитывать изменение D f , происходящее с f(x, у), если х переходит в х+ D х, а у переходит в y+Dy. Будем предполагать, что Dx и Dy бесконечно малы:

Последнее уравнение и есть основное соотношение, связываю­щее приращение Df с Dx и Dy.

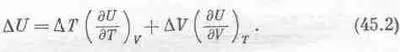
Посмотрим, как используется это соотношение; для этого вычислим изменение внутренней энергии U(Т,V ), если тем­пература Т переходит в Т+ D T , а объем V переходит в V+DV. Используем формулу (45.1) и запишем