Ричард Фейнман - 4. Кинетика. Теплота. Звук

Так как кривая 4 описывает адиабатическое сжатие от d до а, то

Т 1 V a g -1 =T 2 V d g -1 . (44.6а)

Если поделить эти равенства одно на другое, то мы выясним, что отношения V b /V a и V c /V d равны, поэтому равны и лога­рифмы в (44.4) и (44.5). Значит,

Q 1/T 1=Q 2/T 2. (44.7)

Это и есть то соотношение, которое мы искали. Хотя оно дока­зано для машины с идеальным газом, мы уже знаем, что оно справедливо для любой обратимой машины.

А теперь посмотрим, как можно вывести этот универсальный закон на основании только логических аргументов, не интере­суясь частными свойствами веществ. Предположим, что у нас есть три машины и три температуры Т 1 , Т 2 и Т 3 . Одна машина поглощает тепло Q 1 при температуре T 1, производит работу W 13 и отдает тепло Q 3 при температуре T 3 (фиг. 44.8).

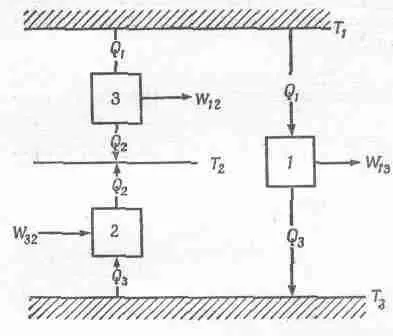
Фиг. 44.8. Спаренные машины 1 и 2 эквивалентны машине 3.

Другая машина работает при перепаде температур t 2 и Т 3 . Предположим, что эта машина устроена так, что она поглощает то же тепло Q 3 при температуре Т 3 и отдает тепло Q 2. Тогда нам придется затратить работу W 32, ведь мы заставили машину работать в обратном направлении. Цикл первой машины заклю­чается в поглощении тепла Q 1и выделении тепла Q 3 при тем­пературе Т 3 . Вторая машина в это время забирает из резер­вуара то же самое тепло Q 3 при температуре T 3 и отдает его в резервуар с температурой Т 2 . Таким образом, чистый резуль­тат цикла этих спаренных машин состоит в изъятии тепла Q l при температуре Т 1 и выделении тепла Q 2при температуре T 2. Эти машины эквивалентны третьей, которая поглощает тепло Q l при температуре Т 1 , совершает работу W 12 и выделяет тепло Q 2при температуре Т 2 . Действительно, исходя из первого за­кона, можно сразу же показать, что W 12=W 13- W 32 :

W 13 -W 32 =(Q 1 -Q 3 )=(Q 2 -Q 3 )=Q 1 -Q 2 =W 12 . (44.8)

Теперь можно получить закон, связывающий коэффициенты полезного действия машин. Ведь ясно, что между эффективностями машин, работающих при перепаде температур Т 2 -T 3 , t 2 -Т 3 и Т 1 -Т 2 , должны существовать определенные соотно­шения.

Сформулируем пояснее наши аргументы. Мы убедились, что всегда можем связать тепло, поглощенное при температуре T 1 и тепло, выделенное при температуре T 2, определив тепло, выделенное при какой-то другой температуре T 3 . Это значит, что мы можем описать все свойства машины, если введем стан­дартную температуру и будем анализировать все процессы с помощью именно такой стандартной температуры. Иначе говоря, если мы знаем коэффициент полезного действия машины, рабо­тающей между температурой Т и какой-то стандартной темпе­ратурой, то сможем вычислить коэффициент полезного действия машины, работающей при любом перепаде температур. Ведь мы рассматриваем только обратимые машины, поэтому ничто не мешает нам спуститься от начальной температуры к стандарт­ной, а потом снова вернуться к конечной температуре. Примем температуру в один градус за стандартную. Для обозначения выделяемого при стандартной температуре тепла используем особый символ Q s . Это значит, что если машина поглощает при температуре Т тепло Q, то при температуре в один градус она выделяет тепло Q S . Если какая-то машина, поглощая тепло Q 1 при T 1 , выделяет тепло Q S при температуре в один градус, а другая машина, поглотив тепло Q 2 при Т 2 , выделяет то же самое тепло Q S при температуре в один градус, то машина, поглощающая Q 1 при Т 1 , должна при температуре Т 2 выделять тепло Q 2 . Мы уже доказали это, рассмотрев три машины, ра­ботающие при трех температурах. Таким образом, для полного описания работы машин нам остается узнать совсем немного. Мы должны выяснить, сколько тепла Q 1 должна поглотить ма­шина при температуре T 1 , чтобы выделить при единичной тем­пературе тепло Q S . Конечно, между теплом Q и температурой Т существует зависимость. Легко понять, что тепло должно воз­растать при возрастании температуры, ведь мы знаем, что если заставить работать машину в обратном направлении, то при более высокой температуре она отдает тепло. Легко также по­нять, что тепло Q 1должно быть пропорционально Q S . Таким образом, наш великий закон выглядит примерно так: Каждому количеству тепла Q S , выделенного при температуре в один градус, соответствует количество тепла, поглощенного машиной при температуре Т, равное Q S , умноженному на не­которую возрастающую функцию Q температуры:

Q=Q S f(T). (44.9)

§ 5. Термодинамическая температура

Пока мы не будем делать попыток выразить эту возрастаю­щую функцию в терминах делений знакомого нам ртутного гра­дусника, а взамен определим новую температурную шкалу. Когда-то «температура» определялась столь же произвольно. Мерой температуры служили метки, нанесенные на равных расстояниях на стенках трубочки, в которой при нагревании расширялась вода. Потом решили измерить температуру ртут­ным термометром и обнаружили, что градусные расстояния уже не одинаковы. Сейчас мы можем дать определение температуры, не зависящее от каких-либо частных свойств вещества. Для этого мы используем функцию f(T), которая не зависит ни от одного устройства, потому что эффективность обратимых машин не зависит от их рабочего вещества. Поскольку найденная нами функция возрастает с температурой, то мы можем считать, что она сама по себе измеряет температуру, начиная со стандартной температуры в один градус. Для этого надо только договориться, что

Q=Q S T, (44.10)

а

Q S =S · 1°. (44.11)

Это означает, что теперь мы можем найти температуру тела, определив количество тепла, которое поглощается обратимой машиной, работающей в интервале между температурой тела и температурой в один градус (фиг. 44.9)

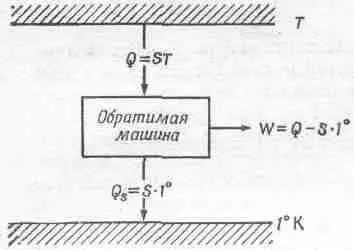
Фиг. 44.9. Абсолютная термо­динамическая температура.