Александр Филиппов - Многоликий солитон

Если точка А движется по гиперболе так, что площадь S равномерно растет со временем, т. е. S = ω 0 t , то x ( S ) = exp(ω 0 t ), а y ( S ) = 1/ x ( S ) = exp(-ω 0 t ). С помощью этого построения легко найти производную показательной функции. Площадь Δ S бесконечно малого прямоугольника x ( S ) AA'x ( S + ΔS) равна [ x ( S + Δ S ) - x ( S )] y ( S ) = Δ S , откуда следует, что

[ x ( S + Δ S ) - x ( S )]1/Δ S = 1/ y (S) = x ( S ),

т. е. Δ( e S )/Δ S = е S . Когда S = ω 0 t , то отсюда следует, что

Δ( e S )/Δ t = Δ x /Δ t = ω 0 e ω 0 t ,

т. е. х' = ω 0 х . Точно так же у' = -ω 0 у , и мы показали, что у = ехр (-ω 0 t ) — решение уравнения (4.7). Самое общее решение можно получить, если взять S = ω 0( t + t 0), т. е. просто сдвинуть начало отсчета времени.

Аналогия с геометрическим определением тригонометрических функций cos(ω 0 t ) и sin(ω 0 t ) теперь должна быть ясной. Они определялись как проекции на координатные оси точки, движущейся по окружности единичного радиуса. Поэтому площадь сектора, «заметаемого» радиусом, также равномерно нарастала со временем: S = ω 0 t .

Еще ближе аналогия тригонометрических функций с гиперболическими функциями. Построим на таком же рисунке, как и рис. П1 взаимно перпендикулярные оси ОУ и ОХ (рис. П2).

Поделенные на 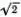проекции X ( S ) и Y ( S ) точки А на эти оси называются гиперболическим синусом и гиперболическим косинусом аргумента S и обозначаются следующим образом:

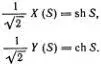
Эти функции похожи на sin S и cos S . Ясно, что их легко выразить через ехр ( S ) и ехр (- S ), но полезно знать и геометрическое определение, исходя из которого можно найти все основные свойства показательной и гиперболических функций.

Самое главное свойство показательной функции, которое можно было бы взять за определение, выражается очень просто: e S 1+ S 2= e S 1 • e S 2 . Доказывается оно геометрическим рассуждением, провести которое мы предлагаем читателю. Покажите также, что sh S = 1/2 ( e S - e -S ), ch S = 1/2 ( e S + e -S ).

2. Найдем теперь геометрическим построением решение уравнения (4.6). Обозначим = ψ (рис. ПЗ).

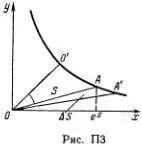
Отсюда очевидно, что ψ = (π - φ)/4 и tg ψ = exp(- S )/exp( S ) = exp(-2 S ). Приращение площади ΔS при малом смещении точки А по гиперболе можно записать как площадь малого сектора с радиусом ( ОА ) 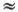( ОА' ) и углом -Δψ = 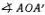, т. е. Δ S = -½Δψ·( ОА ) 2. Так как ( ОА ) = ехр( S )/cos ψ, то отсюда следует, что

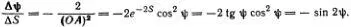
Возвращаясь к углу φ, находим, что

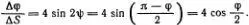
Чтобы получить отсюда уравнение (4.6), достаточно положить S = ½ω 0 t . Тогда φ ' = 2ω 0cos(φ/2), а условие tgψ = exp(-2 S ) дает

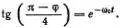
Мы показали, что угол φ( t ) зависимость которого от t определена этим уравнением, удовлетворяет уравнение (4.6). Общее решение уравнения (4.6) можно найти сдвигом начала отсчета времени, т. е. заменой в формуле (4.9) t на t + t 0. Если угол φ близок к π, то для α = (π - φ)/4 получим из (4.9), что α = ехр(-ω 0 t ) (так как tg α 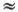α). Таким образом, α удовлетворяет уравнению (4.7).

3. В заключение приведем некоторые солитонные уравнения и их простейшие решения.

Уравнение КдФ написано на с. 217, а его солитонное решение на с. 222, формулы (7.1), (7.2). Обычно это уравнение записывают для безразмерной функции u = 3 y /4 h от безразмерных переменных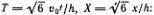

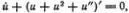
где точка обозначает производную по Т , а штрих — производную по X . Солитонное решение в новых переменных

u = 6 k /ch 2[ k ( Х - VT )],

где k — произвольное число, а V = 1 + 4 k 2(сравните это с (7.1) и (7.2)). Если заменить в уравнении КдФ и u 2на u З, то получим модифицированное уравнение КдФ (или мКдФ), также часто встречающееся в приложениях. Его солитонное решение имеет простой вид

u = 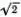k /ch [ k ( Х - VT )], V = 1 + k 2.

Уравнение «синус-Гордона» приведено в тексте на с. 181, формула (6.11). Обычно его записывают для функции u = π + φ от безразмерных переменных Т = ω 0 t и Х = ω 0 x / v 0:

Как следует из (6.5), его односолитонное решение имеет вид

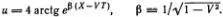
Два солитона описываются решением

u = 4 aгctg [ V sh (β X )/ch (β VT )],

солитон-антисолитон решением

u = 4 aгctg [ V -1sh (β VT )/ch (β Х )],

а бризер есть

u = 4 aгctg [ α sin ( ЬТ )/ Ь сh ( αХ )], α 2+ Ь 2= 1.

Приведем еще солитонное решение уравнений цепочки Тоды:

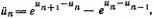
где u n — безразмерные координаты частиц в цепочке. Солитонное решение этих уравнений описывается формулами

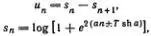
α — произвольное число. Заметим, что дискретизованное уравнение КдФ имеет вид

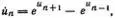
а уравнения Тоды в континуальном пределе приводят к уравнению Буссинеска

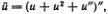
которое иногда называют уравнением нелинейной струны.

Наконец, полезно знать простейшее уравнение нелинейной диффузии (Хаксли)

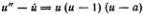
и его решение в виде уединенной волны