Б. Карлов - Учебник, судоводителя-любителя

Для определения точек на земной поверхности ее принято мысленно делить вертикальными и горизонтальными плоскостя ми, образующими с поверхностью земли линии – меридианы и параллели. Концы воображаемой оси вращения земли называются полюсами – северным, или нордовым, и южным, или зюйдовым.

Меридианы – большие круги, проходящие через оба полюса. Параллели – малые круги на земной поверхности, параллельные экватору.

Экватор – большой круг, плоскость которого проходит через центр земли перпендикулярно оси ее вращения.

Как меридианов, так и параллелей на земной поверхности можно вообразить бесчисленное множество. Экватор, меридианы и параллели образуют сетку географических координат земли.

Место любой точки А на земной поверхности можно определить по ее широте ( f ) и долготе ( l ).

Широтой места называется дуга меридиана от экватора до параллели данного места. Иначе: широта места измеряется центральным углом, заключенным между плоскостью экватора и направлением из центра земли на данное место. Широта измеряется в градусах от О до 90° по направлению от экватора к полюсам. При расчетах считают, что северная широта f N имеет знак плюс, южная широта – f S знак минус.

Разностью широт ( f 1 – f 2 ) называется дуга меридиана, заключенная между параллелями данных точек (1 и 2).

Долготой места называется дуга экватора от нулевого меридиана до меридиана данного места. Иначе: долгота места измеряется дугой экватора, заключенной между плоскостью нулевого меридиана и плоскостью меридиана данного места.

Разностью долгот ( l 1 -l 2 ) называется дуга экватора, заключенная между меридианами заданных точек (1 и 2).

Нулевой меридиан – гринвичский меридиан. От него производится измерение долготы в обе стороны (к востоку и западу) от 0 до 180°. Западная долгота отсчитывается на карте влево от гринвичского меридиана и при расчетах берется со знаком минус; восточная – вправо и имеет знак плюс.

Широта и долгота любой точки на земле называются географическими координатами этой точки.

Мысленно воображаемая горизонтальная плоскость, проходящая через глаз наблюдателя, называется плоскостью истинного горизонта наблюдателя, или истинного горизонта (рис. 38).

Предположим, что в точке А находится глаз наблюдателя, линия ZABC – отвесная, HH 1 – плоскость истинного горизонта, а линия P NP S – ось вращения земли.

Из множества вертикальных плоскостей только одна плоскость на чертеже будет совпадать с осью вращения земли и точкой А. Пересечение этой вертикальной плоскости с поверхностью земли дает на ней большой круг P N BEP SQ , называемый истинным меридианом места, или меридианом наблюдателя. Плоскость истинного меридиана пересекается с плоскостью истинного горизонта и дает на последней линию норд-зюйда NS . Линия OW , перпендикулярная линии истинного норд-зюйда, называется линией истинного оста и веста (востока и запада).

Таким образом, четыре основные точки истинного горизонта – север, юг, восток и запад – занимают в любом месте на земле, кроме полюсов, вполне определенное положение, благодаря чему относительно этих точек можно определять различные направления по горизонту.

Направления N (север), S (юг), О (восток), W (запад) носят название главных румбов. Вся окружность горизонта делится на 360°. Деление производится от точки N по движению часовой стрелки.

Промежуточные направления между главными румбами называются четвертными румбами и носят наименование NO , SO , SW , NW . Главные и четвертные румбы имеют следующие значения в градусах:

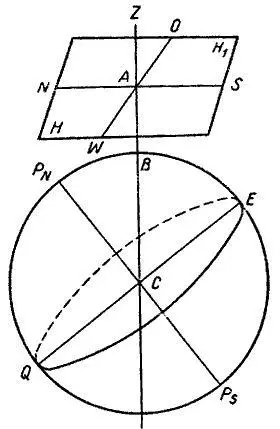
Рис. 38. Истинный горизонт наблюдателя

N – 0° SO -135° W -270°

NO -45° S – 180° NW-315 0

O – 90° SW – 225°

Видимое с судна водное пространство ограничивается окружностью, образованной кажущимся пересечением небесного свода с поверхностью воды. Эта окружность называется видимым горизонтом наблюдателя. Дальность видимого горизонта зависит не только от высоты расположения глаз наблюдателя над водной поверхностью, но и от состояния атмосферы.

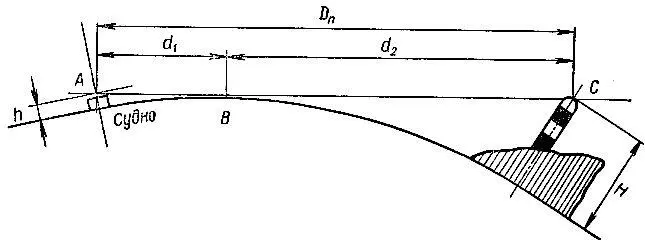
Рис 39. Дальность видимости предмета

Судоводитель всегда должен знать, как далеко он видит горизонт в разных положениях, например, стоя у штурвала, на палубе, сидя и т. п.

Дальность видимого горизонта определяется по формуле:

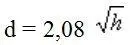
или, приближенно, для высоты глаза наблюдателя менее 20 м по формуле:

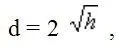
где d – дальность видимого горизонта в милях;

h – высота глаза наблюдателя, м.

Пример. Если высота глаза наблюдателя h = 4 м, то дальность видимого горизонта 4 мили.

Дальность видимости наблюдаемого предмета (рис. 39), или, как ее называют, географическая даль ность D n , является суммой дальностей видимого горизонта с высоты этого предмета Н и высоты глаза наблюдателя А.

Наблюдатель А (рис. 39), находящийся на высоте h , со своего судна может видеть горизонт только на расстояние d 1 , т. е. до точки В водной поверхности. Если же поместить наблюдателя в точке В водной поверхности, то он мог бы видеть маяк С, расположенный от него па расстоянии d 2 ; поэтому наблю датель, находящийся в точке А, увидит маяк с расстояния, равного D n :

D n= d 1+d 2.

Дальность видимости предметов, расположенных выше уровня воды, можно определить по формуле:

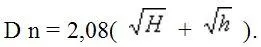
Пример. Высота маяка H = 16,8 м, высота глаза наблюдателя h = 4 м.

Решение. D n = l 2,6 мили, или 23,3 км.

Дальность видимости предмета определяется также приближенно по номограмме Струйского (рис. 40). Прикладывая линейку так, чтобы одной прямой были соединены высоты, соответствующие глазу наблюдателя и наблюдаемому предмету, получают на средней шкале дальность видимости.

Пример. Найти дальность видимости предмета высотой над уровнем моря в 26,2 м при высоте глаза наблюдателя над уровнем моря в 4,5 м.

Решение. D n = 15,1 мили (пунктирная линия на рис. 40).

На картах, лоциях, в навигационных пособиях, в описании знаков и огней дальность видимости дана для высоты глаза наблюдателя 5 ж от уровня воды. Так как на маломерном судне глаз наблюдателя расположен ниже 5 м, для него дальность видимости будет меньше обозначенной в пособиях или на карте (см. табл. 1).

Пример. На карте обозначена дальность видимости маяка в 16 миль. Это значит, что наблюдатель увидит этот маяк с расстояния 16 миль, если его глаз будет на высоте 5 м над уровнем моря. Если же глаз наблюдателя находится на высоте 3 м, то видимость соответственно уменьшится на разность дальности видимости горизонта для высот 5 и 3 м. Дальность видимости горизонта для высоты 5 м равна 4,7 мили; для высоты 3 м – 3,6 мили, разность 4,7 – 3,6=1,1 мили.