Григорий Гутнер - Философия. Античные мыслители

Далее Никомах описывает свойства каждого из трех видов, чем мы здесь заниматься уже не будем. Заметим, что такая классификация четных чисел для современной математики не очень интересна, тогда как пифагорейцы явно придают ей большое значение. Чем же она важна? Я думаю, что некоторую подсказку мы получим, если посмотрим, как определяет эти виды чисел Евклид.

Четно-четное число есть четным числом измеримое четное число раз.

Четно-нечетное число есть четным числом измеримое нечетное число раз.

Нечетно-четное число есть нечетным числом измеримое четное число раз (Евклид. Начала. VII. Опр. 8-10).

Получается, что речь здесь, как и при изучении геометрических фигур, идет об измеримости. На этот раз одно число оказывается мерой для других. Помимо того, что все числа измеримы единицей и, следовательно, соизмеримы, между числами определенного вида можно найти дополнительную соизмеримость, т. е. можно измерить их общей мерой, отличной от единицы. Измеримость же есть составленность целого из частей, более того, определенная организация частей, составляющих целое. У каждого из трех видов четных чисел эта организация разная.

Туже мысль можно увидеть и в классификации нечетных чисел. Здесь так же различаются три вида, причем так, что два из них противоположны, а третий – промежуточный. Числа первого из этих видов называются «первичными и несоставными», второго – вторичными и составными. Числа третьего вида Никомах определяет как «сами по себе вторичные и составные, но по отношению к другим – первичные и несоставные».

Первый из названных видов мы теперь называем простыми числами. Эти числа делятся лишь на себя и на единицу, т. е. измеримы лишь единицей.

Числа второго вида, противоположного первому, «могут быть измерены другим числом, помимо единицы» [47] iy. [Никомах, 113 ]. . Это составные числа, т. е. нечетные числа, имеющие отличные от единицы делители. Таковы, например, 9,15, 25.

Что касается третьего вида, то его описание у Никомаха весьма неясно и содержит явные логические неувязки. Например, он относит число 9 и ко второму, и к третьему виду.

Мы не будем, чтобы не затягивать наш рассказ, излагать все основы пифагорейской арифметики. Заметим лишь, что выявляемые в ней свойства чисел всегда будут определяться одной и той же указанной только что мыслью: очередное установленное свойство числа есть следствие некоторой организации частей внутри целого. При этом организация частей определяется их соразмерностью.

Обратим лишь еще раз внимание на различение четного и нечетного, принципиальное для всей пифагорейской арифметики.

Четные числа делимы на две равные части. Нечетные числа неделимы надвое «из-за присутствия единицы в середине» [48] [ Никомах юб]. .

Что означает «присутствие единицы в середине» легко понять из графического изображения четного и нечетного числа:

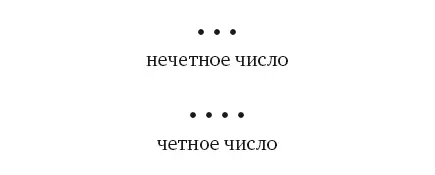
Рис.3. Представление четных и нечетных чисел

Нечетное число имеет центр симметрии, а у четного в центре ничего нет. Эта пустота в центре делает четное число как бы неустойчивым, делимым и, как следствие, менее совершенным, чем нечетное. Нечетное число имеет начало, конец и середину и представляет собой замкнутое целое. Четному же числу свойственна разомкнутость. Оно как будто растекается в бесконечность. Во всяком случае, пифагорейцы полагали, что нечетному числу соответствует предел, а четному – беспредельное.

Обратим внимание, что и в этом случае все определяется организацией частей в пределах целого. Однако, говоря о числе, мы должны обратить внимание на другую пару понятий, более общих, чем часть и целое. Эти понятия – единство и множество. Число, как мы видели, было определено как множество, составленное из единиц. Такое множество, конечно, есть нечто целое, состоящее из частей. Но оно представляет собой предельный случай такого целого. В геометрии, космологии и музыке части были сложны и соразмерны. Здесь же они просты и неразличимы. Все сводится к многократному повторению одного и того же. При любой соразмерности мы имеем такое повторение. Но общая мера, воспроизводимая много раз в пределах целого, все же есть нечто сложное. Она также имеет собственное устройство. Число – идеальная модель целого, состоящего из соразмерных частей. Общая мера в нем предельно проста и уже не имеет никакой собственной организации. Всякая общая мера есть усложненная единица. Число, следовательно, лежит в основе всех других целостностей. Всякая организованная, упорядоченная сложность имеет в своей основе число. Оно являет эту сложность (сложенность) в самом чистом виде. Можно сказать и иначе: всякое целое, состоящее из частей, есть, по своей сути, число, усложненное, обремененное какими-то дополнительными, нечисловыми характеристиками. Поэтому истинное знание всякого сущего представляет собой знание его числовой структуры. Поэтому арифметика есть главная наука, без которой невозможна никакая другая.

На примере пифагорейской арифметики мы далее попробуем уточнить, что такое ясное знание и каковы его условия. Мы уже не раз говорили о структурировании целого. Знание целого состоит в усмотрении организации его частей. Чтобы объяснить смысл такого усмотрения нам будут полезны дополнительные сведения о пифагорейской теории чисел.

Прежде всего заметим, что слово «усмотрение» имеет здесь буквальный смысл. Число для пифагорейцев имеет зримое выражение, оно всегда имеет явное графическое представление. Выше мы уже воспользовались одним из таких представлений, чтобы показать различие между нечетным и четным числом. Число как множество, составленное из единиц, всегда можно созерцать, видеть глазами, как целое, объединяющее свои части. Однако такое созерцание требует определенной работы. Рассмотрим, например, число 9, которое исходно представляет собой девять собранных вместе единиц. Выглядеть это может, например, так:

Пока что перед нами лишь собрание единиц, в котором мы не видим никакой особой структуры. Впрочем, можно сразу заметить, что перед нами число – нечетное, т. е. имеющее начало, середину и конец. Наше созерцание приобретает большую определенность. Мы уже выделили некоторую внутреннюю структуру.

Далее мы заметим, что выбранное нами число представляет собой трижды повторенную тройку:

В исходном целом обнаруживается дополнительная структура, обусловленная выделением других частей, из которых оно составлено. Чтобы сделать эту структуру более явной, запишем число в таком виде: