Пользователь - Мастер и Маргарита: гимн демонизму? либо Евангелие беззаветной веры

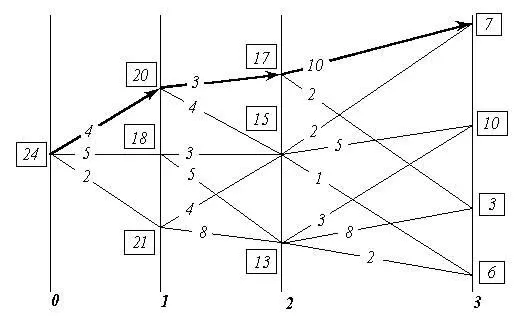
и запоминается максимальный полный выигрыш и соответствую-

щий ему переход (фрагмент траектории). Максимальный полный

350

Глава 6. Достаточно общая теория управления (в крат-

ком изложении)

выигрыш для каждого из состояний во множестве «2» взят в пря-

моугольную рамку, а соответствующий ему переход отмечен стрел-

кой. Таких оптимальных переходов из одного состояния в другие,

которым соответствует одно и то же значение полного выигрыша, в

принципе может оказаться и несколько. В этом случае все они в

методе неразличимы и эквивалентны один другому в смысле по-

строенного критерия оптимальности выбора траектории в про-

странстве параметров, которыми описывается система.

После этого множество «2», предшествовавшее завершающему

процесс множеству «3», можно рассматривать в качестве завер-

шающего, поскольку известны оценки каждого из его возможных

состояний (максимальные полные выигрыши) и дальнейшая опти-

мизация последовательности шаговых управлений и выбор опти-

мальной траектории могут быть проведены только на ещё не рас-

смотренных множествах, предшествующих множеству «2» в опти-

мизируемом процессе (т.е. на множествах «0» и «1»).

Таким образом, процедура, иллюстрируемая рис. 2, работо-

способна на каждом алгоритмическом шаге метода при переходах

из n -го в (n — 1) -е множество, начиная с завершающего N -ного

множества до начального состояния системы.

В результате последовательного попарного перебора множеств,

при прохождении всего их набора, определяется оптимальная по-

следовательность преемственных шаговых управлений, макси-

мально возможный полный выигрыш и соответствующая им тра-

ектория. На рис. 3 утолщённой линией показана оптимальная тра-

ектория для рассматривавшегося примера.

351

Основы социологии

РИС. 3. К СУЩЕСТВУ МЕТОДА ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ.

ОПТИМАЛЬНАЯ ТРАЕКТОРИЯ.

В рассмотренном примере критерий оптимальности — сумма

шаговых выигрышей. Но как было отмечено ранее, критерий опти-

мальности может быть построен и как произведение обязательно

неотрицательных сомножителей.

Поскольку результат (сумма или произведение) не изменяется

при изменении порядка операций со слагаемыми или сомножите-

лями, то алгоритм работоспособен и при переборе множеств воз-

можных состояний в порядке, обратном рассмотренному: т.е. от ис-

ходного к завершающему множеству возможных состояний.

Если множества возможных состояний упорядочены в хроноло-

гической последовательности, то это означает, что расчётная схема

может быть построена как из реального настоящего в прогнозируе-

мое определённое будущее, так и из прогнозируемого определённо-

го будущего в реальное настоящее. Это обстоятельство говорит о

двух неформальных соотношениях реальной жизни, лежащих вне

алгоритма метода:

1. Метод динамического программирования формально алгорит-

мически нечувствителен к характеру причинно-следственных

обусловленностей (в частности, он не различает причин и

следствий). По этой причине каждая конкретная интерпрета-

ция метода в прикладных задачах должна строиться на нефор-

мальном учёте реальных обусловленностей следствий причи-

нами.

352

Глава 6. Достаточно общая теория управления (в крат-

ком изложении)

2. Если прогностика в согласии с иерархически наивысшим все-

объемлющим управлением, а частное управление, вложенное

во всеобъемлющее управление, осуществляется квалифици-

ровано, в силу чего процесс частного управления протекает в

ладу с иерархически наивысшим всеобъемлющим управле-

нием, то НЕ СУЩЕСТВУЕТ УПРАВЛЕНЧЕСКИ ЗНАЧИМОЙ

РАЗНИЦЫ МЕЖДУ РЕАЛЬНЫМ НАСТОЯЩИМ И ИЗ-

БРАННЫМ БУДУЩИМ.

Процесс целостен, по какой причине ещё не свершившееся,

но уже нравственно избранное и объективно не запрещённое

Свыше будущее, в свершившемся настоящем защищает тех, кто

его творит на всех уровнях: начиная от защиты психики от на-

важдений до защиты от целенаправленной «физической» агрес-

сии. То есть, если матрица возможных состояний (она же матри-

ца возможных переходов) избрана в ладу с иерархически выс-

шим объемлющим управлением, то она сама — защита и ору-

жие, средство управления, на которое замкнуты все шесть прио-

ритетов средств обобщённого оружия и управления (см. раздел

8.5).

Объективное существование матриц возможных состояний и

переходов проявляется в том, что в слепоте можно «забрести» в не-

кие матрицы перехода и прочувствовать на себе их объективные

свойства. Последнее оценивается субъективно, в зависимости от

отношения к этим свойствам, как полоса редкостного везения либо

как нудное «возвращение на круги своя» или полоса жестокого не-

везения.

Но для пользования методом динамического программирова-

ния и сопутствующими его освоению неформализованными в ал-

горитме жизненными проявлениями матриц перехода , необходимо

СОБЛЮДЕНИЕ ГЛАВНОГО из условий:

В задачах оптимизации процессов управления метод динами-

ческого программирования <���реального будущего: — по умолча-

нию> работоспособен только, если определён вектор целей

управления, т.е. должно быть избрано завершающее процесс

определённое состояние .

В реальности это завершающее определённое состояние долж-

но быть заведомо устойчивым и приемлемым процессом, объем-

лющим и несущим оптимизируемый методом частный процесс. Но

353

Основы социологии

выбор и определение определённых характеристик процесса, в ко-

торый должна войти управляемая система по завершении алгорит-

ма метода, лежит вне этого метода — в области «мистики» или в

области методов, развитых в нематематических по своему суще-

ству науках и ремёслах.

«Каково бы ни было состояние системы перед очередным ша-

гом, надо выбирать управление на этом шаге так, чтобы вы-

игрыш на данном шаге плюс оптимальный выигрыш на всех

последующих шагах был максимальным», — Е.С. Вентцель,

«Исследование операций. Задачи, принципы, методология».

(Москва, «Наука», 1988 г., с. 109).

Неспособность определить вектор целей управления (достиже-

нием которого должен завершиться оптимизируемый в методе

процесс) и (или) неспособность выявить исходное состояние