Юрий Кочинев - Аудит: теория и практика

Практика показывает, что при осуществлении описанных выше оценок перед аудитором неизбежно встают вопросы: как соотнести полученные качественные оценки факторов с качественной оценкой анализируемого риска? Как соотнести качественную оценку аудиторского риска с качественной оценкой его компонентов?

Например, аудитор оценивает неотъемлемый риск R НТ исходя из трех градаций (низкий, средний, высокий риск). Для осуществления этой оценки аудитор проанализировал ряд влияющих на неотъемлемый риск факторов (опыт и квалификация главного бухгалтера, его загруженность, масштаб бизнеса, сложность хозяйственных операций, стабильность нормативной базы и т. д.). Несколько факторов получили низкую оценку, несколько – среднюю, несколько – высокую. Как оценить неотъемлемый риск?

Другой пример: по оценке аудитора неотъемлемый риск – средний, контрольный риск – средний, риск необнаружения – низкий. Как оценить аудиторский риск?

Ответы на эти вопросы можно получить, осуществив качественную оценку компонентов аудиторского риска с помощью метода, основанного на теории нечетких множеств. Рассмотрим его.

Процедуры рассмотренных выше оценок могут быть формализованы применением метода, основанного на теории нечетких множеств. Рассмотрим возможность подобной формализации на примере оценки неотъемлемого риска R НТ

Полное множество значений риска R НТразобьем на три подмножества:

• низкий риск;

• средний риск;

• высокий риск.

Введем понятие показателя степени риска G, принимающего значения от нуля до единицы.

Соответствующее множеству R НТмножество G также разобьем на три подмножества:

• низкая степень риска;

• средняя степень риска;

• высокая степень риска.

Далее построим классификацию текущего значения g показателя степени риска G, соответствующую разбиению этого множества на подмножества (табл. 3.7).

Построение указанной выше классификации осуществляется путем экспертной оценки (оценки аудитора) и в зависимости от его профессионального суждения может отличаться от варианта, предложенного в табл. 3.7.

Таблица 3.7.Классификация текущих значений показателя степени неотъемлемого риска

Далее введем следующие обозначения: X – анализируемый фактор, определяющий значение степени риска; N – количество факторов; i – текущий номер фактора (1 ≤ i ≤ N).

Рассмотрим какой-либо фактор X (например, «опыт и квалификация главного бухгалтера»). Принадлежность элементов нечеткого множества X. определенному интервалу значений g (низкой, средней или высокой степени риска) установим с помощью функции принадлежности, областью определения которой является носитель g, а областью значений – единичный интервал [0, 1]. В теории нечетких множеств обычно используют трапециевидные или треугольные функции принадлежности. В нашем случае целесообразно применение прямоугольных функций принадлежности, представленных на рис. 3.8, где λ ij– уровень принадлежности фактора X iнечеткому подмножеству множества G (низкой, средней или высокой степени риска), j – номер подмножества (j = 1, 2, 3).

Далее введем понятие коэффициента значимости каждого фактора, обозначив его r i.

Путем экспертной оценки (т. е. на основании профессионального суждения аудитора) определим, равнозначны или неравнозначны выбранные нами факторы.

Если факторы равнозначны, то коэффициенты значимости равны друг другу и могут быть определены из следующего выражения:

Если факторы неравнозначны, то их следует путем экспертных оценок проранжировать в порядке убывания их влияния. Тогда коэффициенты значимости факторов могут быть определены по правилу Фишберна:

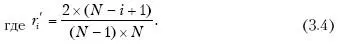
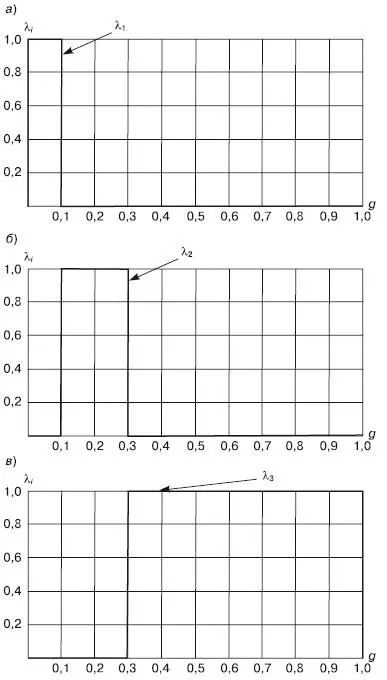
Рис. 3.8.Функции принадлежности фактора X: а – низкому риску; б – среднему риску; в – высокому риску

Затем для каждого фактора X iопределяем λ ij– уровень принадлежности фактора интервалу значений g (низкой, средней или высокой степени риска). Текущее значение λ ij= 1, если согласно профессиональному суждению аудитора X iпринадлежит данному интервалу, и λ ij= 0 в противном случае.

Далее определяем значение показателя степени риска g исходя из полученных текущих значений λ ijи коэффициентов значимости факторов r i:

где g j– центральные значения показателя степени риска для каждого интервала:

g 1= 0,05; g 2= 0,20; g 3= 0,65.

Полученное из формулы (3.5) значение показателя степени риска g определяет подмножество RНТ (низкий, средний или высокий риск).

Рассмотрим применение данного метода на конкретном примере.

Пример.Аудитор выделил пять факторов, определяющих, по его мнению, неотъемлемый риск, и проранжировал их в порядке убывания влияния:

Коэффициенты значимости факторов определены аудитором по формулам (3.3) и (3.4):

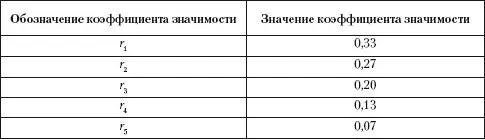
Результаты аудиторских процедур опроса, наблюдения, просмотра документов показали, что фактор X 1соответствует низкому риску (опытный главный бухгалтер); X 2– высокому (главный бухгалтер перегружен); X 3– среднему (документооборот организован на среднем уровне);

X 4– высокому (нормативная база нестабильна); X 5– высокому (наличие сложных операций).

Исходя из полученных результатов аудитор определил уровни принадлежности факторов:

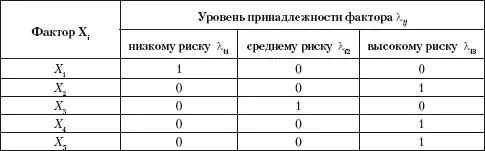
Искомое значение показателя степени риска определяется по формуле (3.5):

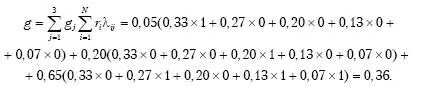
По классификации текущих значений показателя степени риска (табл. 3.7) получаем значение R НТ: неотъемлемый риск – высокий.