Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews
- Название:Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews
- Автор:
- Жанр:
- Издательство:КНОРУС; ЦИПСиР
- Год:2011
- Город:Москва
- ISBN:978-5-406-01441-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews краткое содержание
Для всех, кто интересуется валютным рынком, собирается зарабатывать или уже зарабатывает на этом рынке, хочет научиться делать прогнозы по курсам валют. Для валютных инвесторов, трейдеров и студентов, будущая профессия которых связана с работой в банке, финансовой компании или с операциями на финансовых и товарных рынках.
Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
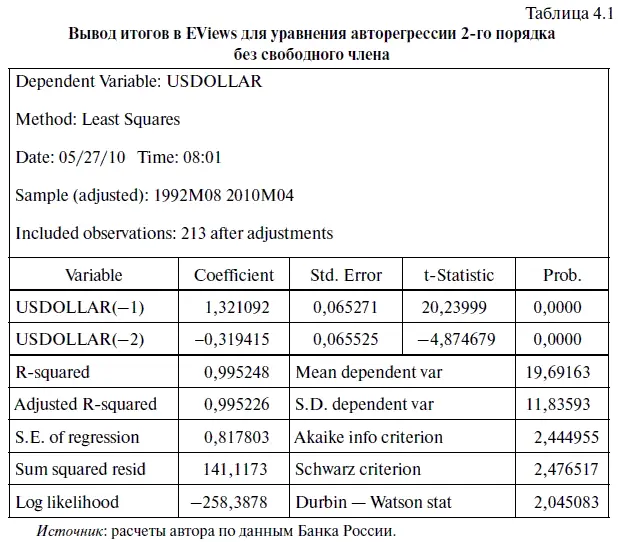
4.2. Оценка точности прогностической модели, проверка остатков на автокорреляцию и стационарность
Далее проверим уравнение AR(2) без константы на наличие автокорреляции в остатках с помощью LM-теста Бройша — Годфри, используя при этом алгоритм действий № 7. При этом в мини-окне LAG SPECIFICATION зададим величину лага, равную 2, поскольку мы тестируем уравнение авторегрессии 2-го порядка. Полученные результаты занесем в табл. 4.2. Поскольку значимость ( Probability ) главного критерия этого теста «Наблюдения × R 2»(Obs × R-squared) равна 0,1069, то, следовательно, нулевая гипотеза об отсутствии автокорреляции в остатках не может быть отклонена с 95 %-ным уровнем надежности (а точнее сказать, с 89,31 %-ным уровнем надежности). Если сравнить последнюю цифру с аналогичными данными табл. 3.4, то об отсутствии автокорреляции в остатках в последнем случае можно говорить с большей уверенностью.
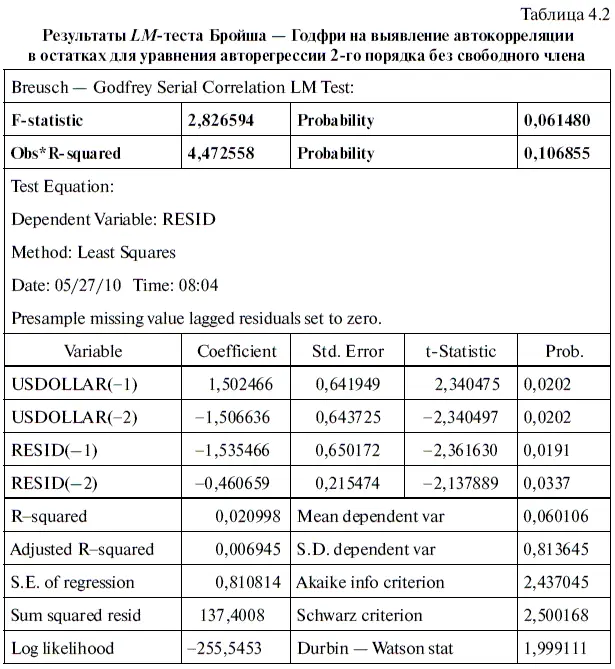
Таким образом, сравнение параметров, с одной стороны, уравнения AR(2) с константой (см. табл. 3.3), а с другой стороны, уравнения AR(2) без константы (см. табл. 4.1) не помогло нам сделать окончательный вывод в пользу одного из них. Аналогичный результат у нас получился и по итогам проведения LM-теста Бройша — Годфри на наличие автокорреляции в остатках. Поэтому мы решили оценить точность прогнозов, сделанных с помощью уравнения авторегрессии без константы, воспользовавшись алгоритмом действий № 8 «Как оценить точность статистической модели в EViews». В результате получилась табл. 4.3.
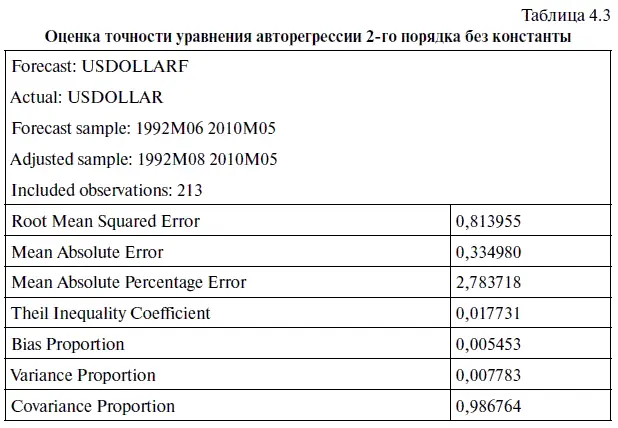
Если сравнить табл. 4.3 с табл. 3.6, то можно легко прийти к выводу, что шесть из восьми параметров, характеризующих точность прогнозов, свидетельствуют в пользу уравнения авторегрессии с константой. Правда, при этом разница между ними была весьма незначительной. Однако вполне естественно, что при прогнозировании курсов валют нас в первую очередь интересует точность предсказаний, которую можно получить с помощью той или иной статистической модели. И с этой точки зрения уравнение авторегрессии 2-го порядка без константы оказалось точнее. Так, средняя ошибка прогноза по модулю у последней модели оказалась (после округления) равна 33,50 коп., а средняя ошибка по модулю (%) — 2,78 %, т. е. соответственно на 2,5 коп. и на 2,02 процентного пункта ниже, чем у уравнения авторегрессии с константой. Именно это обстоятельство и побудило нас сделать выбор в пользу уравнения авторегрессии без константы.
Чтобы сделать адекватный прогноз по курсу доллара, необходимо учесть как тренд, так и случайную компоненту, поскольку оба этих фактора существенно влияют на динамику валюты. Судя по табл. 4.3, нам удалось построить уравнение авторегрессии, с достаточно высокой степенью точности учитывающее тренд. Используя эту статистическую модель, можно делать точечные прогнозы, которые, правда, очень редко совпадают с фактическим курсом доллара. Объясняется это тем, что в ежемесячных колебаниях курса доллара достаточно большую роль играет не только тренд, но и случайная компонента. Судя по тому, что средняя ошибка по модулю равна 2,78 %, вполне очевидно, что эту цифру можно считать своего рода среднестатистическим индикатором вклада случайной компоненты в динамику курса доллара.
Поскольку точечный прогноз по определению не в состоянии указать нам диапазон вероятного отклонения фактического курса доллара от его предсказываемого значения, то с этой целью приходится использовать так называемый интервальный прогноз. Суть интервального прогнозирования заключается в определении интервала значений, в который прогнозируемое значение попадет с определенной долей вероятности. Чем выше интервал прогноза (разница между максимальным и минимальным значениями прогноза), тем больше вероятность (ее еще называют уровнем надежности) его реализации.
Однако прежде чем перейти к составлению интервальных прогнозов, нам необходимо, во-первых, проверить полученные остатки на стационарность, во-вторых, посмотреть, является ли распределение остатков нормальным.
В EViews проверить остатки на стационарность достаточно просто, для этого нужно только точно следовать алгоритму действий № 9.
С этой целью нужно выбрать строку 2 WORKFILE (рабочий файл), а затем открыть файл RESID (остатки), который появляется в рабочем файле после того, как мы воспользовались опцией FORECAST (см. алгоритм действий № 8 «Как оценить точность статистической модели в EViews»).
Далее в файле RESID нам следует воспользоваться опцией UNIT ROOT TEST (тест на единичный корень), в результате чего появится (рис. 4.1) мини-окно UNIT ROOT TEST, в котором нам нужно выбрать следующие опции.
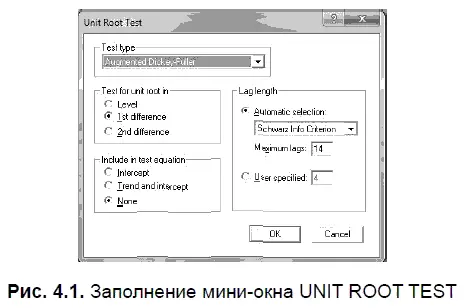
Параметр TEST TYPE (тип теста) установим на опции AUGMENTED DICKEY — FULLER (расширенный тест Дикки — Фуллера), поскольку этот тест чаще всего используется на практике, так как он учитывает возможную автокорреляцию в остатках. Параметр TEST FOR UNIT ROOT IN (тест на единичный корень для…) следует установить на опции 1ST DIFFERENCE (первых разностей), так как при исследовании остатков на стационарность не используются их исходные уровни. Параметр INCLUDE IN TEST EQUATION (включить в тестовое уравнение) установим на опции NONE (не включать тренд или тренд и константу), поскольку в остатках отсутствует тренд и свободный член уравнения (константа). Параметр LAG LENGTH (длина лага) установим на опции AUTOMATIC SELECTION (автоматический выбор), что позволит EViews самостоятельно выбрать длину лага. Вполне естественно, что при необходимости длину лага можно задать самому.
Теория тестирования стационарности временных рядов изложена ниже. А чтобы просто сделать вывод о стационарности временн o го ряда на основе расширенного теста Дикки — Фуллера, нужно знать следующее. После того как ранее мы заполнили мини-окно Unit Root test и щелкнули кнопку ОК, в результате у нас получилась табл. 4.4 с итогами теста. При этом главное внимание нужно обратить на верхнюю строчку теста, выделенную жирным шрифтом: Augmented Dickey — Fuller test statistic (статистика расширенного теста Дикки — Фуллера). Поскольку статистика теста Дикки — Фуллера в этом случае равна 11,05764, а ее значимость (Prob.) равна 0,0000, то нулевая гипотеза о том, что D(RESID) имеет единичный корень, отвергается. Следовательно, мы можем принять альтернативную гипотезу о стационарности полученных остатков.
Читать дальшеИнтервал:
Закладка:









