Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

k — количество параметров, использованных для создания данного временн o го ряда.

После этого значение теста Жарка — Бера сравнивают с распределением χ 2(хи-квадрат) с двумя степенями свободы. В том случае, если критерий Жарка — Бера > χ 2 крипт, то делается вывод о неслучайном характере распределения, а следовательно, нулевая гипотеза о нормальном распределении опровергается. В нашем случае значение теста Жарка — Бера равно 17147,64, а следовательно, если сравнить с соответствующим табличным значением χ 2 крипт 001, 2= 9,21, то рассчитанный нами критерий Жарка — Бера существенно выше последнего.

Впрочем, нам не обязательно заглядывать в таблицу. Чтобы вычислить значимость критерия Жарка — Бера в Excel, достаточно воспользоваться функцией ХИ2РАСП (17147,64; 2) = 0. Ав EViews значимость ( Probability ) критерия Жарка — Бера, равная нулю, выдается автоматически (см. табл. 4.4).

Поскольку при значимости критерия Жарка — Бера (Probability) < 0,05 нулевая гипотеза о нормальном распределении опровергается с 95 % уровнем надежности, то, следовательно, в нашем случае мы вынуждены отвергнуть гипотезу о нормальном распределении остатков.

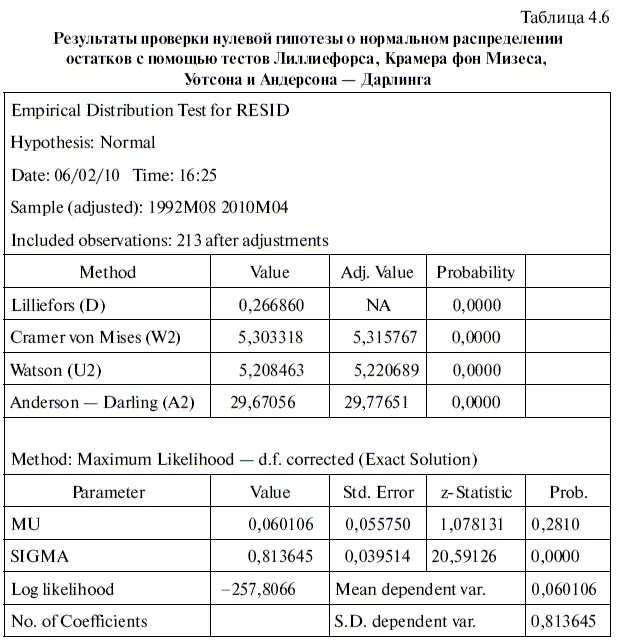
В EViews имеется и ряд других тестов, с помощью которых можно провести дополнительную проверку нулевой гипотезы о нормальном распределении. В частности, если в файле RESID воспользоваться опциями VIEW/DISTRIBUTION/EMPIRICAL DISTRIBUTION TESTS… (смотреть/распределение/тесты на проверку характера эмпирического распределения), то мы получим результаты проверки нулевой гипотезы о нормальном распределении остатков с помощью соответствующих тестов Лиллиефорса (Lilliefors), Крамера фон Мизеса (Cramer von Mises), Уотсона (Watson) и Андерсона — Дарлинга (Anderson — Darling). Результаты тестирования занесены в табл. 4.6. Поскольку значимость (Probability) критериев по всем четырем тестам равна нулю, то нулевая гипотеза о нормальном распределении остатков опровергается.

В связи с опровержением нулевой гипотезы возникает вопрос: можно ли в этой ситуации строить интервальные прогнозы по курсу доллара исходя из предположения о нормальном распределении остатков? Вот как на него отвечает известный американский профессор статистики Стэнфордского университета Т. Андерсон: «Приведенные процедуры проверки гипотез и построения доверительных областей были основаны на предположении о том, что наблюдения распределены нормально. Если предположение о нормальности не выполняется, то эти процедуры все же можно применять для больших выборок, используя асимптотическую теорию…

Значение приведенных теорем (доказывающих асимптотическую теорию. — Прим. авт.) состоит в том, что, опираясь на них, обычную теорию для нормального случая при больших объемах выборок можно использовать с достаточной точностью и в тех ситуациях, когда наблюдения не являются нормально распределенными» [11] Андерсон Т. Статистический анализ временных рядов. С. 35, 39. .

Можно ли применить асимптотическую теорию к распределению остатков, полученных с помощью статистической модели USDOLLAR = а × USDOLLAR(-l) + b × USDOLLAR(-2)? Поскольку малой выборкой принято называть выборку, имеющую до 30 степеней свободы, а в нашей выборке имеется 210 степеней свободы, то вполне естественно, что асимптотическую теорию в этом случае можно использовать.

Почему столь важно строить интервальные прогнозы по курсу доллара исходя из предположения о нормальном распределении остатков? Дело в том, что нормальный закон распределения играет важнейшую роль в теории вероятностей. При этом главной особенностью этого закона является тот факт, что он является предельным законом, к которому — при определенных условиях — приближаются другие законы распределения. Предполагая, что остатки распределены согласно закону о нормальном распределении (т. е. их распределение определяется воздействием множества случайных причин), мы тем самым приписываем им следующие свойства, благоприятные для построения интервальных прогнозов.

Во-первых, график плотностей вероятностей нормального распределения (см. рис. 4.4) имеет колоколообразную форму, симметричную относительно средней (математического ожидания) μ. При этом плотность вероятностей нормального распределения определяется по формуле

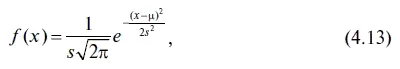
где s — стандартное отклонение.

Следовательно, плотность вероятностей нормального распределения полностью определяется двумя параметрами остатков — их средней величиной (математического ожидания) μ и стандартным отклонением s.

Во-вторых, график плотностей вероятностей нормального распределения показывает, что для нормально распределенных остатков вероятность отклонения от их средней величины (математического ожидания) μ быстро уменьшается с ростом этого отклонения.

В-третьих, если μ = 0, а стандартное отклонение s = 1, то нормальное распределение с такими параметрами называется нормированным. При этом плотность вероятностей нормированного нормального распределения определяется по следующей формуле:

В-четвертых, если функцию нормированной плотности вероятностей распределения f(x) перевести в проценты (при 1 = 100 %), а затем построить график плотности вероятностей нормированного нормального распределения, то мы получим диаграмму, изображенную на рис. 4.5.

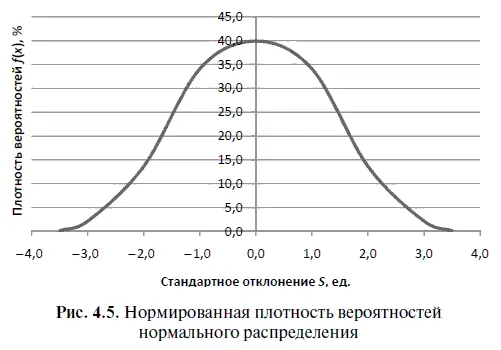
Исходя из этого рисунка можно прийти к выводу: если мы будем суммировать (интегрировать) вероятность попадания остатка в область интервального прогноза при стандартном отклонении s, то выяснится, что в этом случае в область интервального прогноза попадет 68,17 % всех нормально распределенных остатков. Соответственно при стандартном отклонении s = ± 2 в область интервального прогноза попадет 95,45 % всех нормально распределенных остатков, а при стандартном отклонении s = ± 3 в область интервального прогноза попадет 99,73 % всех нормально распределенных остатков. Заметим также, что чаще всего интервальные прогнозы строят исходя из 95 %-ного уровня надежности при нормированном стандартном отклонении, равном 1,96; либо при 99 %-ном уровне надежности при нормированном стандартном отклонении, равном 2,58; либо при 99,9 %-ном уровне надежности при нормированном стандартном отклонении 3,29.