Александр Волошинов - Математика и искусство

Принцип меры носил у древних греков не только формальный структурно-математический характер. Мера для греков — это прежде всего человек, это норма поведения, закон мироздания, структура художественного произведения. Греческое искусство возвеличивало человека даже тогда, когда говорило о богах.

Понятия симметрии, пропорции и ритма играли важную роль в познании греками пространственно-временной структуры окружающего мира. Закономерность и красота мироздания раскрывались перед ними и в симметрии живых организмов, и в пропорциональности человеческого тела, и в ритмах чередования дня и ночи, смены времен года и т. д. Вся античная архитектура и скульптура воплощали в себя эти принципы красоты. Блестящими примерами тому служат и величественные пропорции Парфенона, и знаменитый "Канон" Поликлета — скульптура и теоретический трактат, в которых автор попытался воплотить идеальные" по его мнению, пропорции мужского тела.

Поликлет. Дорифор (копьеносец), или Канон. Ок. 440 до н. э. Римская копия с утраченного оригинала. В пропорциях статуи воплощен закон золотого сечения

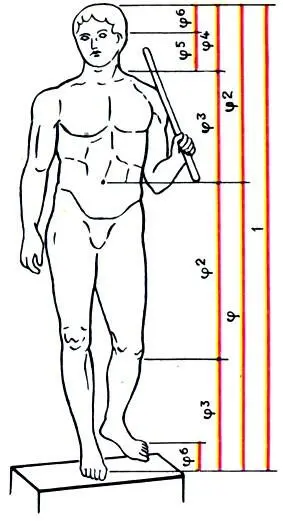
Приведен математический анализ пропорций Канона

Ведь назначение и цель гармонии — упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту.

Не менее содержательным было и античное понятие гармонии. В древнегреческой философии гармония в противоположность хаосу означала организованность Вселенной. Гармония трактовалась не как внешнее объединение разрозненных частей, а как внутреннее их единство, как единство противоположностей предела и беспредельного, частей и целого. Пифагор, не только великий математик, но и основоположник античной эстетики, считал, что гармония "внутренне присуща вещам, из которых составлен мир". Ее только нужно извлечь из вещей, что и делает художник благодаря своему мастерству, уму и таланту. В главе 7 мы познакомимся с пифагорейским учением о гармонии сфер, согласно которому расстояния между планетами соответствуют числовым отношениям музыкальной гаммы и весь космос звучит единым благозвучным аккордом. Вообще, пифагорейцы благоговели перед количественной картиной мира, выраженной в числе. Это была своеобразная философия числа, о которой мы расскажем в главе 5. Понятию гармонии древнегреческий философ Платон придал социальное значение, рассматривая гармонию как совокупность физических достоинств и высоких нравственных принципов человека-гражданина. Отсюда пошло выражение "гармонически развитая личность".

Разумеется, античная эстетика не решила всех проблем. Так, оставалось непонятным, откуда возникает субъективизм и релятивизм в эстетических оценках (типа "На вкус и цвет товарищей нет"), если прекрасное едино. Однако античное учение о мере и гармонии как объективных признаках прекрасного прошло через эпохи средневековья, Возрождения, Просвещения вплоть до наших дней, хотя происхождение красоты в каждую эпоху трактовалось по-своему. Во времена средневековья для философа Фомы Аквинского красота заключалась в боге, который "именуется прекрасным как причина гармонии и ясности". Как отголоски этой веры в божественное происхождение прекрасного сохранились выражения "ангельское лицо", "божественный голос", "чудесная погода". Для ренессансного гуманиста Альберти гармония есть "абсолютное и первичное начало природы". Французские просветители-материалисты также подчеркивали природную основу красоты.

С тех пор как в 1844 г. К. Маркс впервые высказался о "законах красоты" (см. с. 26), о них заговорили как о чем-то давно известном, не утруждая себя необходимостью раскрыть содержание этих законов. Между тем дальше того, что в данном вопросе эстетики разделились на два противоборствующих лагеря "природников" и "общественников", дело не пошло. Проблема законов красоты в эстетике скорее только поставлена, но не решена. Однако то, что законы меры и гармонии являются объективными законами прекрасного, по которым природа стихийно, а человек сознательно формируют материю, создавая совершенные формы, является бесспорным.

Остановимся несколько подробнее на эстетическом удержании законов симметрии, пропорциональности и гармонии как слагаемых прекрасного. Что касается закона ритма, который проявляется и в музыке, и в архитектуре, и в изобразительном искусстве, и в стихосложении, то он заслуживает отдельного разговора и в данной книге рассматриваться не будет.

4.1. Симметрия.Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863-1945), "слагалось в течение десятков, сотен, тысяч поколений". "Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм". Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А. В. Шубникова (1887-1970).

Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о "соразмерности", что и означает в переводе с греческого слово "симметрия", с течением времени приобрело универсальный характер и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — поворотной, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Благодаря последней симметрии все физические приборы (в том числе будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, бы царила на Земле неразбериха, если бы эта симметрия была нарушена!