Александр Волошинов - Математика и искусство

Итак, симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью, т. е. воспринимается как красота. Простой пример убеждает в этом. Чернильная клякса сама по себе некрасива. Но стоит перегнуть лист бумаги с невысохшей кляксой пополам, и мы получим кляксу, которая уже производит приятное впечатление. Зеркальная симметрия новой кляксы, т. е. закономерное расположение ее частей, и определяет красоту нашей "рукотворной" кляксы. Знание законов геометрической симметрии сделает такие поиски быстрыми и плодотворными.

Чувство глубочайшего уважения к мощи законов симметрии никогда не ослабевает у того, кто обдумывал изящество и красоту безупречных математических доказательств и сопоставлял это со сложными и далеко идущими физическими и философскими следствиями.

На рисунке изображены узоры, полученные с использованием различных типов геометрической симметрии из простой, достаточно бесформенной кляксы. Узор на рисунке б получен с помощью зеркальной симметрии. Однако закон его построения слишком прост и очевиден, потому и эстетическая ценность такого узора невелика.

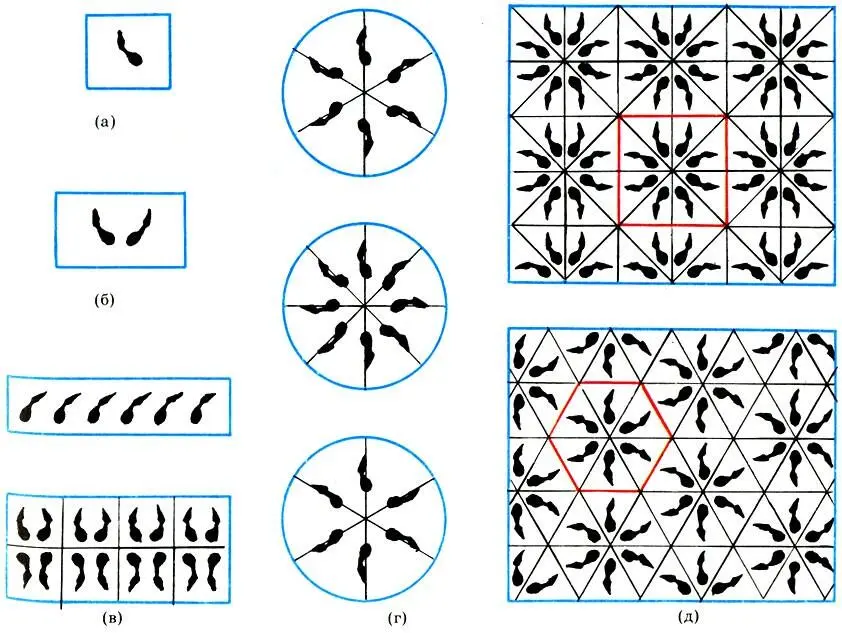
'Кляксография' — узоры, полученные из обыкновенной кляксы (а) с помощью зеркальной симметрии (б), переносной симметрии (в)у поворотной симметрии (г) и орнаментальной симметрии(d)

Узоры, приведенные на рисунке в, называются бордюрами и представляют собой тип переносной симметрии, когда каждая предыдущая фигура совпадает с последующей при поступательном перемещении вдоль бордюра на постоянный интервал (шаг симметрии). Нижний бордюр имеет более сложный закон построения, чем простая переносная симметрия. Всего же существует семь типов бордюров.

На рисунке г показаны так называемые "розетки". Розетки получаются поворотом фигуры вокруг вертикальной оси на угол 360°/n (n = 2, 3, 4, ...), т. е. обладают поворотной симметрией n-го порядка. (Верхняя розетка имеет поворотную симметрию 6-го порядка, средняя — 8-го, нижняя же сочетает зеркальную и поворотную симметрии, но в то же время она имеет чисто поворотную симметрию 3-го порядка.)

Наконец, на рисунке д показаны два орнамента из семнадцати возможных. Орнаментальная симметрия строится на одной из пяти возможных плоских решеток. Верхний орнамент имеет квадратную решетку, а нижний — гексагональную (правильный шестиугольник). Заполнив одну ячейку решетки, мы получим с помощью переносной симметрии весь орнамент.

Вот так с помощью симметрии простая клякса превращается в затейливые узоры, которые уже никак не назовешь некрасивыми. Нам нравится вглядываться в узоры симметрии, постигать их законы, и они воспринимаются нами как красивые. "Смысл эстетического воздействия симметрии (и всякой иной закономерности), по нашему мнению,- писал Шубников,- заключается в том психическом процессе, который связан с открытием ее законов".

Другим важным фактором, составляющим эстетическое содержание симметрии, является ее целесообразность , которая также есть проявление закономерного. Уже первобытные люди понимали, что симметричные орудия более целесообразны, чем несимметричные. Таким образом, уже в эпоху неолита симметрия была выделена как наиболее совершенная форма, о чем свидетельствуют многочисленные украшения с симметричными рисунками.

Современный человек просто не в состоянии представить себе несимметричный (а значит, и нефункциональный) самолет или автомобиль. В этой связи показательны наблюдения известного летчика-испытателя, Героя Советского Союза Марка Галлая: "Я заметил, что красивая, ласкающая своими пропорциями взор машина обычно к тому же и хорошо летает. Эта, на первый взгляд, почти мистическая закономерность имеет, я думаю, свое вполне рациональное объяснение: дело, по-видимому, обстоит как раз наоборот — хорошо летающая машина начинает представляться "красивой". Эстетическое формируется под влиянием рационального".

Симметрия, пропорция, гармония — слагаемые прекрасного

Итак, целесообразность симметричных форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно, и красоты. Идея связи прекрасного с симметрией пронизывала всю греческую философию, все греческое искусство. Достаточно вспомнить строго симметричные формы античных архитектурных памятников, изумительную стройность греческих ваз, математическую строгость их орнамента. С тех пор симметрия и красота в сознании человека слиты воедино. В "Фаусте" Гёте противопоставляет в образах Прекрасной Елены и одноглазой, однозубой старухи Форкиады красоту симметрии и уродство асимметрии. В "Сказке о царе Салтане" Пушкин рисует величавую Царевну-Лебедь со звездой во лбу (красота-симметрия) и окривевших злодеек ткачиху с поварихой (уродство-асимметрия). В "Войне и мире" Льва Толстого мы читаем: "Это был огромный, в два обхвата, дуб, с обломанными, давно видно, суками и с обломанной корой, заросшей старыми болячками. С огромными своими неуклюже, несимметрично растопыренными корявыми руками и пальцами, он старым, сердитым и презрительным уродом стоял между улыбающимися березами".

Симметрия как объективный признак красоты проходит через всю историю искусств. "Равенство, неравенство, повторение и симметрия, определенные структуры играют в искусстве, как и в математике, фундаментальную роль",- считает физик Гейзенберг. Не говоря уже об архитектуре и скульптуре, симметрия господствует в изобразительном искусстве Древнего Египта, Древней Греции и Рима, средневековья и Возрождения. Зеркальная симметрия была особенно излюблена шумерами.

Симметрия в искусстве. Зеркальная симметрия: нагрудное украшение с именем фараона. XX в. до н. э. (а)

Симметрия в искусстве. Зеркальная симметрия: капитель колонны из дворца Артаксеркса II в Сузах. V-IV вв. до н. э. (б)

Поворотная симметрия 12-го порядка: мозаика купола баптистерия в Равенне. V в. (в)