Александр Волошинов - Математика и искусство

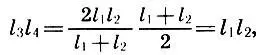(6.5)

откуда, разделив обе части на l 1 2, получаем второй важный вывод:

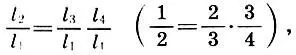(6.6)

или

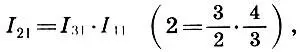
т. е. октава есть произведение квинты на кварту.

Разделив же (6.5) на l 1l 3, Архит получает и третью из основных пропорций -геометрическую:

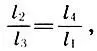(6.7)

которую называли "музыкальной": октава так относится к квинте, как кварта к основному тону .

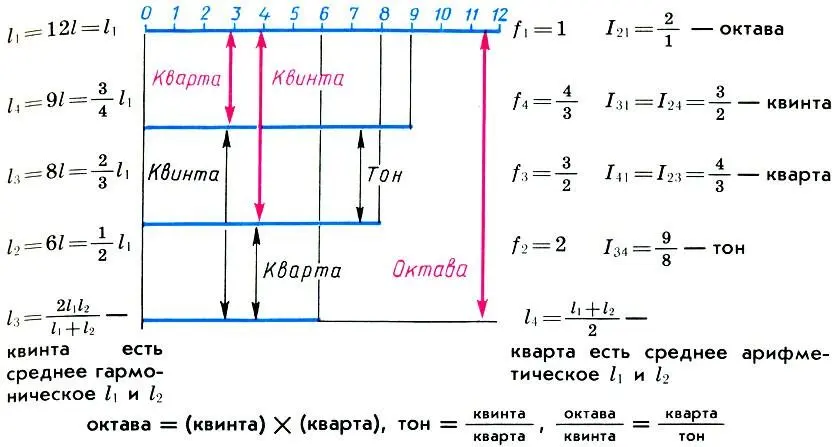
Деление струны монохорда (l 1) на части, образующие с ней совершенные консонансы: октаву (l 2), квинту (l 3) и кварту (l 4) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками

Легко получить еще два соотношения:

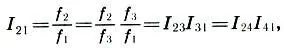(6.8)

т. е. октава делится на два неравных консонансных интервала — квинту и кварту . Интервал, дополняющий данный интервал до октавы, называется его обращением . Таким образом, квинта есть обращение кварты и наоборот.

Наконец, найдем интервальный коэффициент между струнами квинты l 3и кварты l 4, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):

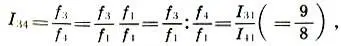(6.9)

т. е. тон-интервал равен отношению квинты к кварте .

Заметим, что в отличие от обычного Расстояния на прямой r 21= х 2— x 1определяемого как разность координат конца и начала, интервальный коэффициент — вЫсотное расстояние — определен как отношение составляющих его тонов 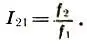Тогда три тона f 123, расположенных на равных расстояниях r и образующих арифметическую прогрессию x 1, х 2= x 1+ r, x 3= x 1+ 2r. Поэтому интервальные коэффициенты складываются и вычитаются "геометрически", а сами интервалы — "арифметически", как обычные расстояния, а именно:

сумма двух интервалов равна произведению их интервальных коэффициентов:

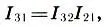(6.10)

разность двух интервалов равна частному их интервальных коэффициентов:

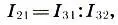(6.11)

разделить интервал на n равных частей означает извлечь корень степени n из его интервального коэффициента:

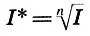(6.12)

и т. д.

Чтобы перейти от интервальных коэффициентов к интервалам-расстояниям, достаточно ввести логарифмический интервал L = log aI и логарифмическую частоту F = log af. Тогда, логарифмируя определение (6.1) и равенства (6.10) — (6.12) получаем привычное определение и правила действия с расстояниями:

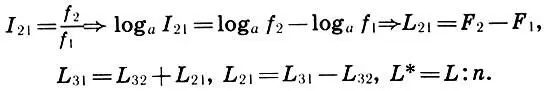(6.13)

В главе 9 при построении равномерно-темперированного строя особенно удобно будет взять логарифмы по основанию 2. Тогда интервал октавы f 1= 1, f 2= 2 перейдет в логарифмический интервал 0≤L≤1 (log 2l=0, log 22 = l).

Решение проблемы деления октавы подсказало Архиту сразу два доказательства иррациональности 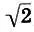. В самом деле, если попытаться разделить октаву на два равных интервала I, то, полагая в (6.8) I 23= I 31= I, имеем

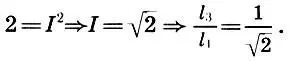
Но при таком соотношении длин струн прослушивается явный диссонанс. Поскольку же консонанс определяется отношением целых чисел вида (n+1):2, то напрашивается мысль, что число 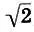не может быть выражено отношением двух целых чисел, т. е. является иррациональным.

Второе доказательство иррациональности 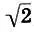менее музыкально, но более математично. Чтобы найти квадратный корень числа, не являющегося полным квадратом, Архит разлагает его на два неравных сомножителя (2 = 1*2), затем образует из этих сомножителей среднее арифметическое 3/ 2и среднее гармоническое 4/ 3и составляет из этих чисел музыкальную пропорцию (6.7):

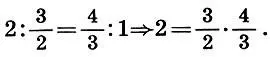
Произведение средних членов этой пропорции равно данному числу 2, а их разность 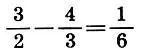меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно, 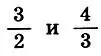можно рассматривать как приближенные значения .

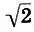( 3/ 2с избытком, 4/ 3с недостатком ] .

Проделав ту же процедуру над первыми приближениями, получим вторые приближения:

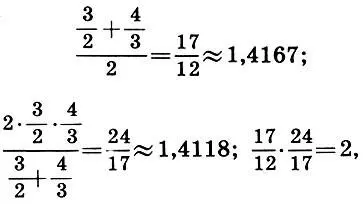
причем

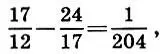
а затем — и третьи приближения:

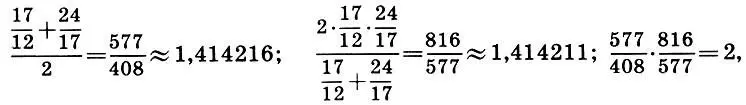
причем

1,414216-1,414211=0,000005.

Поскольку данную процедуру можно повторять неограниченно, то ясно, что число 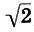иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение 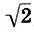равно 1,414213..., мы видим, что "музыкальный" метод Архита очень быстро сходится к точному значению 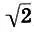и уже третье приближение дает пять верных знаков после запятой!

Но вернемся к нашим интервалам. Итак, октава делится на два неравных консонанса квинту и кварту, а квинта — на консонанс кварту и диссонанс тон. Тон-интервал и был принят за интервал между соседними по высоте звуками (ступенями) при построении пифагоровой гаммы. Здесь и находится ключ к построению лада. По мнению советского музыковеда Л. А. Мазеля, интервал квинты, разделенный на кварту и тон, является основным музыкальным элементом. Выбрав тон в качестве основной ладообразующей ступеньки, античным теоретикам осталось только отложить от основного звука 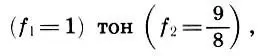, затем — еще один тон 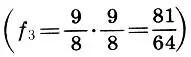, а оставшийся интервал между вторым тоном и тоном кварты 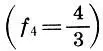назвать полутоном 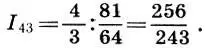Название это вполне оправдано, так как деление тона-интервала пополам по формуле (6.12) дает 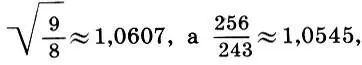т. е. полутон практически равен половине тона *. Так была получена основа всей древнегреческой музыки — тетрахорд — четырехструнный звукоряд в пределах кварты.