Александр Волошинов - Математика и искусство

*( Интервал, тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами. )

Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:

дорийский: полутон — тон — тон;

фригийский: тон — полутон — тон;

лидийский: тон — тон — полутон .

Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.

Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли "гармония". Именно в античной теории музыки слово "гармония" обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:

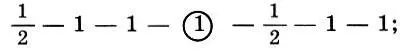
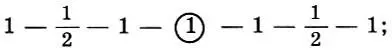
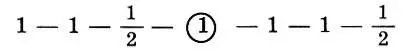
Здесь 1 обозначает тон, 1/2 — полутон, разделительный тон обведен кружком. Эти античные гармонии сопоставимы с современными гаммами. В самом деле, каждый, знакомый с азами музыкальной грамоты, узнает в лидийской гармонии обычный натуральный мажор (2 тона — полутон, 3 тона — полутон, или на белых клавишах фортепиано до - ре - ми - фа - соль - ля - cи - дo ), а в дорийской и фригийской — почти натуральный минор *.

*( "Почти" потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая. )

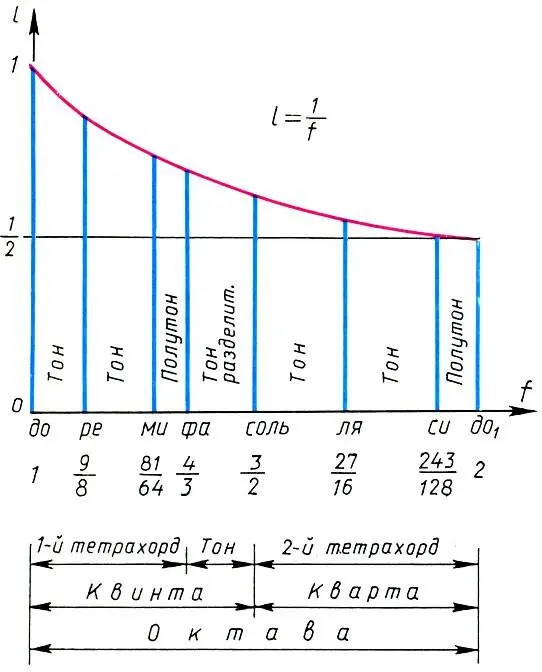
Пифагоров строй лидийской гаммы и его математические характеристики

Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f 1= 1, oнаходим первый тетрахорд: f 1= 1, f 2= 9/ 8, f 3= 9/ 8* 9/ 8= 81/ 64, f 4= 4/ 3. Второй тетрахорд получается сдвигом первого на квинту: f 5= 3/ 2f l= 3/ 2, f 6= 3/ 2f 2= 27/ 16, f 7= 3/ 2f 3= 243/ 128, f 8= 3/ 2f 4= 2. Окончательно для интервальных коэффициентов имеем

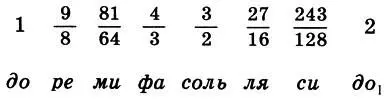(6.14)

Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.

Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики "склеивали" тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах. Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.

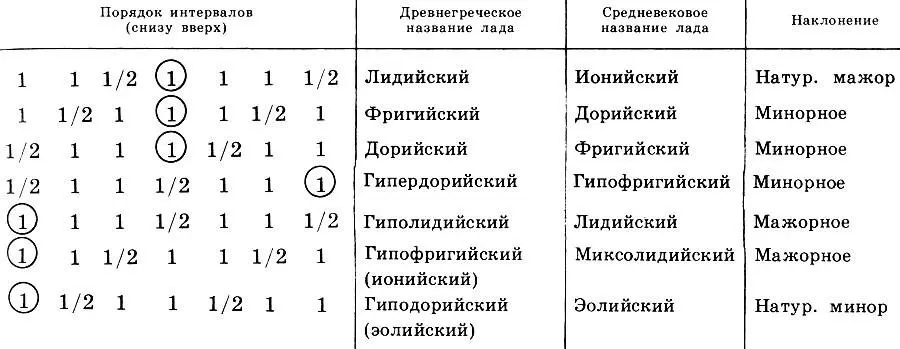
Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения

Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его "этосом", устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.

Пляшущая менада. Рельеф

Так, развивая в работе "Государство" теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: "Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке". Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, "платонический" идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.

Аристотель в "Политике" судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную "этическую" классификацию ладов, различая пады, которые вызывают психическое равновесие (дорийский), напротив, нарушают зго (гипофригийский — "застольный" лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).