Александр Волошинов - Математика и искусство

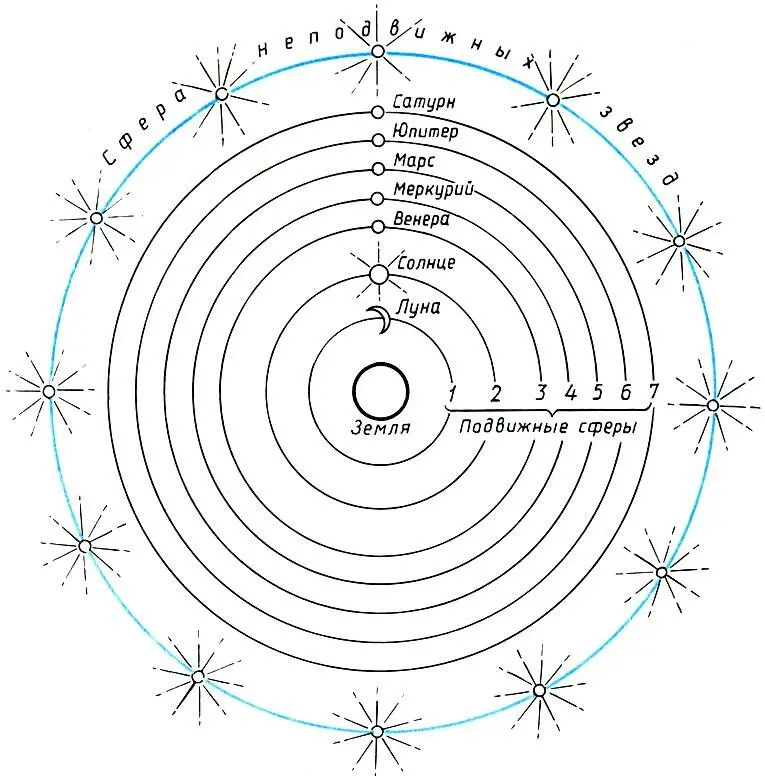
Система мира по Платону

На базе этой системы мироздания Платон развивает теорию небесного гептахорда — семиструнника , т. е. теорию семи подвижных сфер, настроенных в музыкальных отношениях. Согласно Платону, творец Вселенной — Демиург, создав вещество Вселенной, разделил его на две части: одна часть пошла на построение сферы неподвижных звезд, а вторая была математически строго разделена на семь частей для образования сфер Луны, Солнца и пяти планет. По этому поводу в "Тимее" Платона мы читаем: "Делить же он начал следующим образом: прежде всего отнял от целого одну долю, затем вторую — вдвое большую, третью — в полтора раза больше второй и в три раза больше первой, четвертую — вдвое больше второй, пятую — втрое больше третьей, шестую — в восемь раз больше первой, а седьмую — больше первой в двадцать семь раз". В результате получился ряд чисел

1 2 3 4 9 8 27, (7.1)

описывающий гармонию небесных сфер, или небесный гептахорд. Однако ни порядок расположения сфер, несущих светила, ни порядок отсчета чисел в ряде (7.1) Платоном указан не был. Поэтому на протяжении последующих двух тысячелетий члены платонова гептахорда имели самую разнообразную физическую интерпретацию.

Самым простым и соблазнительным было трактовать числа (7.1) как относительные расстояния от Земли до Луны, Солнца, Венеры, Меркурия, Марса, Юпитера и Сатурна соответственно. Тогда эти числа представляли и относительные высоты тонов, так как высота тона, издаваемого сферой, мыслилась пропорциональной скорости вращения сферы, а скорость вращения — пропорциональной расстоянию до неподвижной Земли. Таким образом, чем дальше находилась планета от Земли, тем больше была ее скорость и тем выше издаваемый ею тон. Скорее всего, эти рассуждения были навеяны простым опытом: камень, раскручиваемый на веревке, со свистом разрезает воздух и прекрасно демонстрирует все описанные закономерности. Правда, при такой трактовке относительное расстояние до Марса (9) получалось больше, чем до Юпитера (8), и, чтобы "исправить" эту ошибку, числа 9 и 8 в (7.1) просто переставили. Вот почему во многих текстах платонов гептахорд фигурирует в искаженном виде: 1, 2, 3, 4, 8, 9, 27.

И все-таки оставалось непонятным: откуда вообще взялся этот странный ряд чисел? Это загадка, которую исследователи, начиная с Аристотеля, чаще всего трактовали как некий курьез, если не просто глупость, не требующую даже разъяснений. "Однако,- как справедливо замечал А. Ф. Лосев,- такой антиисторический подход не может быть у современного исследователя, который, конечно, настолько далек от древнего пифагорейства, что даже не испытывает потребности его критиковать, а должен рассмотреть его со всеми объективно-историческими причинами, делающими его существование понятным".

Ключ к Платонову гептахорду, по-видимому, спрятан в самом пифагорейском понимании числа, а именно: единицы — как символа неделимого начала, двойки — как символа неопределенной бесконечности и тройки — как символа определенности. Но для Платона это слишком просто, и в качестве символа беспредельности он берет куб со стороной 2. Тогда его геометрические параметры (длина, площадь грани и объем) дают числа 2, 4, 8. А в качестве символа определенности Платон берет куб со стороной 3 и параметрами 3, 9, 27. Тогда взаимное переплетение этих двух троек чисел плюс начало всего — единица — и дают то единство "беспредельного и определяющих начал", о которых говорил Филолай.

Интересную реконструкцию платонова космоса совсем недавно, в 1985 г., предложил инженер С. В. Житомирский. Учитывая, что небесные сферы мыслились Платоном материально, т. е. обладали некоторой толщиной (такое представление сохранилось вплоть до Кеплера), Житомирский трактует числа (7.1) как толщины соответствующих сфер, причем отсчет начинает не от Земли, как это всегда было принято, а, наоборот, от сферы неподвижных звезд. Далее, вспоминая, что на изготовление последней сферы пошло столько же материала, сколько и на все

остальные, он полагает толщину сферы неподвижных звезд равной толщинам всех остальных сфер, т. е. 54 = 1 + 2 + 3 + 4 + 9 + 8 + 27. Таким образом получается реконструкция картины платонова космоса, которая согласуется с другими космологическими текстами Платона, а числа гептахорда (7.1) наполняются конкретным геометрическим содержанием:

Земля — Луна — Солнце — Венера — Меркурий — Марс — Юпитер — Сатурн — Небо звезд

Заметим, что и реконструкция Житомирского также страдает изъяном, так как Земля теперь растворилась в сфере Луны. Не будем более погружаться в бездну вопросов Платонова космоса, из которых уже два с половиной тысячелетия ищут выхода, и перейдем к музыкальной стороне учения Платона. Легко видеть, что платонов гептахорд содержит в себе все основные музыкальные интервалы: октаву (2/1), квинту (3/2), кварту (4/3), тон (9/8) и полутон 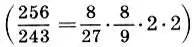. Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до 1-ре 2-до 2-ля 3.

Впрочем, все это сегодня уже неважно. Для нас, людей XX века, важно другое: Платон мыслит мировое пространство неоднородным , как неодинаково натянуты струны единого музыкального инструмента. Но ведь эта мысль о неоднородности мирового пространства созвучна выводам из общей теории относительности Альберта Эйнштейна об искривленности пространства — времени и его неоднородности! Более двух тысячелетий, от Платона до Эйнштейна, мировое пространство мыслилось абсолютным и однородным! И вот за этот огромный промежуток времени, практически равный всей истории европейской цивилизации, наука, как и определено законами диалектики, совершает огромный виток по спирали и прежний вывод делается на базе самых современных научных знаний, а старая научная платформа кажется наивной и смешной! Сколько еще таких витков предстоит сделать науке?!