Александр Волошинов - Математика и искусство

Не менее популярным оставалось в средние века и учение о гармонии сфер. Вообще, считалось, что законы мироздания в основе своей являются музыкальными законами. Мысль эта прочно вошла в сознание не только средневековых ученых-схоластов, но и поэтов. Гармония сфер звучит в "Божественной комедии" великого Данте, написанной в начале XIV века:

Несмотря на увлечение Данте числовой мистикой, архитектура его бессмертной поэмы является непревзойденным образцом математической строгости. Поэма делится на три части: "Ад", "Чистилище" и "Рай". В каждой части — 33 песни, что вместе со вступительной песнью дает 100 песен — квадрат "священного" числа 10 (см. с. 94). В каждой части и каждой песне практически одинаковое число стихов (строк), а каждая часть заканчивается одним и тем же словом — stella (звезда, светило). Описываемое Данте мироздание построено на числе 9 — квадрате символа определенности числа 3: в Аду — 9 кругов, в Раю — 9 небес, семь кругов Чистилища и два уступа предчистилища также дают число девять и т. д.

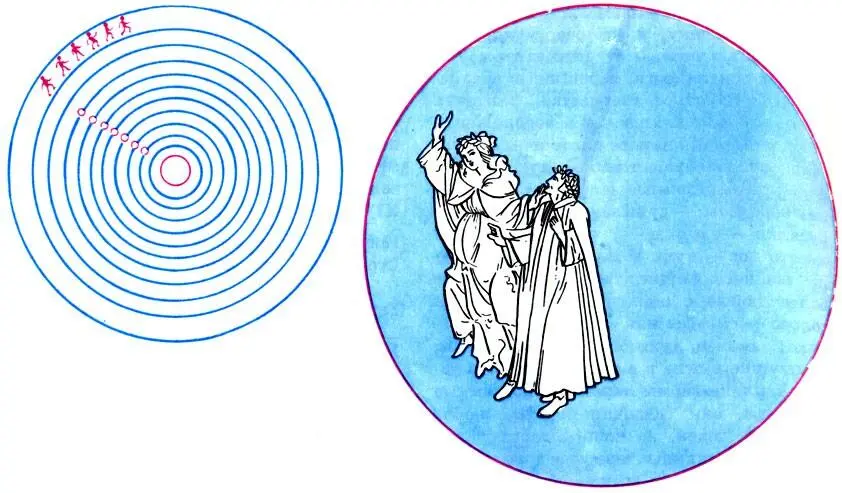
Боттичелли. Иллюстрация к 'Божественной комедии' Данте. 1492-1497. Данте, влекомый Беатриче, взирает на геоцентрическую систему мироздания

Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) — выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы. Но Кеплер поставил и вопросы, достойные отца современного естествознания: почему планет (известных в то время) только шесть? Почему их орбиты имеют те, а не иные параметры?

Сначала молодой учитель математики Иоганн Кеплер тщетно ищет между параметрами планетных орбит простые числовые отношения. Но вдруг... Решая с учениками какую-то геометрическую задачу, он начертил на классной доске равносторонний треугольник со вписанной и описанной окружностями. Внезапно его

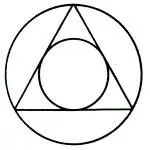
'Космическая музыка': от Платона до Кеплера

озарила мысль, что планетные орбиты связаны между собой посредством геометрических фигур. Однако расчеты показали, что плоские геометрические фигуры не удовлетворяли этой идее. Новые разочарования... "И вот я снова устремился вперед. Зачем рассматривать фигуры

двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений...",- вспоминал впоследствии Кеплер. Новые поиски и новое озарение: существует только шесть планет и, следовательно, пять промежутков между ними. Но и Платоновых тел только пять! Как трудно было допустить, что это простое совпадение!.. "Я еще не имел ясной идеи о порядке, в котором следует расположить правильные тела... День и ночь я проводил за расчетами... Через несколько дней все стало на свои места." Какой накал страстей в этих записях Кеплера!

Вскоре двадцатичетырехлетний учитель издает маленькую книжку с вычур ным названием, как требовала мода того времени,- "Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пр°" порций между небесными кругами и истинных причин числа и размеров небесных сфер, а также периодических движений, изложенный с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком достославной провинции Штирии", или "Mysterium Сosniographicum" ("Тайна мироздания"), как любил называть ее сам Кеплер. Книга эта содержала формулу открытия Кеплера: в сферу орбиты Сатурна Кеплер вписывает куб, в куб — сферу Юпитера, в сферу Юпитера — тетраэдр, и так далее последовательно вписываются друг в друга сферы Марса — додекаэдр, сфера Земля — икосаэдр, сфера Венеры — октаэдр и сфера Меркурия. В центре всей системы коперниканец Кеплер помещает Солнце * . Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа!

*( Для каждого правильного многогранника существует вписанная сфера, касающаяся центров каждой грани, и описанная сфера, проходящая через все вершины, причем центры этих сФер совпадают. Таким образом, все построенные Кеплером сферы имеют общий центр. )

Что же показали математические расчеты? Конечно, совпадение с данными Коперника по радиусам планетных орбит было поразительным, но все-таки не столь точным, как того хотелось бы педантичному Кеплеру [20] Заинтересовавшийся читатель может легко воспроизвести эти расчеты. Например, для куба с ребром а имеем R = a√3/2, r = a/2, откуда R/r = √3 1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны R с = 1,427*10 9 км и R ю = 0,788*10 9 км, откуда R с /R ю = 1,834. По Коgерyику, R с /R ю = 1,758. .Особенно много хлопот доставила Кеплеру сфера Меркурия, которую в конце концов пришлось вписать в октаэдр так, чтобы -она касалась не граней, а середины ребер последнего. Остальные незначительные расхождения между теорией и опытными данными Кеплер объяснил тем, что реальные планетные сферы имеют некоторую толщину, что и позволило "выбрать" эти расхождения.

Однако червь сомнения поселился в Душе Кеплера. Можно сказать, что оставшиеся тридцать лет жизни Кеплер посвятил "спасению" своей теории от самого себя. Эта работа привела к открытию истинных астрономических законов — трех знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер в полной мере не осознал своих настоящих открытий и до конца жизни более всего любил свою первую работу.

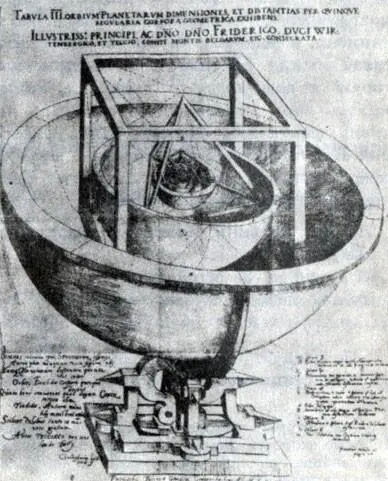
Космический кубок Кеплера, Иллюстрация Иоганна Кеплера из его книги 'Тайна мироздания'. Тюбинген. 1596

Не забыл Кеплер и о самой "музыке" сфер. Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей [21] Из второго закона Кеплера следует, что угловые скорости планет непостоянны и имеют наименьшее значение в афелии и наибольшее — в перигелии. для некоторых планет близки к гармоническим: Марс — 3/2, Юпитер — 6/5, Сатурн — 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс — тенором, Земля и Венера — альтом, а Меркурий — дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.