Александр Волошинов - Математика и искусство

Не следует спешить обвинять Кеплера в мистицизме, богоискательстве, числовых спекуляциях и увлечении отжившими античными теориями. Правильнее видимо, вспомнить о времени, в которое он жил и творил: XVI век закончился костром на площади Цветов в Риме, где 17 февраля 1600 Г. был сожжен Джордано Бруно. Следует вспомнить трагическую историю матери Кеплера, Катерины Кеплер, которую публично объявил ведьмой и процесс над которой тянулся долгие 6 лет. Обвиняемую заковывали в цепи, ставили перед палачом с орудиями пыток, и только искусные действия ее сына Иоганна, который сам вел защиту, позволили выиграть процесс у церковных мракобесов. "Арестованную, к сожалению, защищает ее сын, господин Иоганн Кеплер, математик",- свидетельствовал судебный писец. Только в родном городе Кеплера Вейле с 1615 по 1629 г. ужасная смерть постигла 38 "колдуний". Вот в какое время рождалось современное естествознание!

"Мы имели дело с человеком тонких чувств, всецело и страстно увлеченным поиском пути к более глубокому проникновению в сущность явлений природы, с человеком, который, несмотря на внутренние и внешние трудности, сумел достичь поставленной перед собой возвышенной цели" — так характеризовал личность Кеплера Альберт Эйнштейн, Кеплер XX века, по справедливому определению физиков наших дней.

Заканчивая наше необычное "музыкальное обозрение", перенесемся в 20-е гг. XX века, когда вновь неожиданно зазвучало "пифагорово пенье светил". Согласно теории Нильса Бора, развитой им в 1913 г., движение электрона вокруг атомного ядра возможно только по избранным "разрешенным" орбитам, двигаясь по которым электрон вопреки законам классической электродинамики не излучает энергии, но может скачком переходить с одной орбиты с энергией E iна другую "дозволенную" орбиту с энергией Е k, испуская (i>k) или поглощая (i

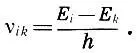(7.2)

h — постоянная Планка.

В простейшем случае атома водорода, содержащего один электрон, энергия n-го энергетического уровня равна

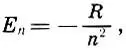(7.3)

R — постоянная Ридберга.

Здесь n = 1, 2, 3,... называется главным квантовым числом. Тогда совокупность частот, излучаемых атомом водорода при переходе с верхнего энергетического уровня на нижний (i>k), определяет спектр испускания данного атома и каждому такому переходу соответствует своя спектральная линия. Для атома водорода согласно формулам 7.2, 7.3 получаем совокупность спектральных линий с частотами

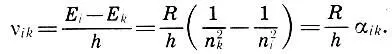
При переходе со второго, третьего и т. д. энергетических уровней n i= 2, 3, 4... на первый n k= 1 получается так называемая "спектральная серия Лаймана", для которой α 21=3/4, α 31=8/9, α 41= 15/16. Но ведь это кварта (3/4), тон (8/9) и полутон в чистом строе (15/16)! "Таким образом,- писал А. Эйнштейн,- мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение".

"То, что нам сегодня удается понять на языке спектров,- это истинная музыка атомных сфер, созвучие целочисленных отношений, все возрастающие порядок и гармония при всем их многообразии — так восторженно отзывался о квантовой теории немецкий физик и математик Арнольд Зоммерфельд (1868-1951).- ... Она представляет собой тот полный таинства инструмент, на котором природа исполняет спектральную музыку и ритмом которого она управляет строением атома и атомных ядер".

Итак, обыкновенная музыкальная гамма увлекла нас вслед за Пифагором, Платоном и Кеплером в путешествие по просторам космоса. Мы узнали, что "пифагорово пенье" услышали и физики XX века, но уже не в космосе, а в противоположной стихии — микромире. Но нам пора от "физических приложений" вновь вернуться к математическому содержанию музыкальной гаммы, которая таит в себе еще немало секретов.

В главе 6 мы получили пифагоров строй, т. е. математическое выражение интервальных коэффициентов, лидийской гаммы (6.14), или, в современной терминологии, пифагоров строй натурального мажора:

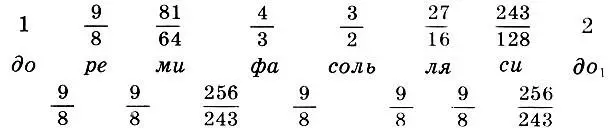(8.1)

Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243 — полутон. Мы обнаружили также, что основные консонансные интервалы в пределах октавы — квинта и кварта — являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:

октава/квинта = кварта/тон.

Таким образом, музыкальная гамма разделена на пропорциональные части; она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.

Прежде всего из (8.1) видно, что расстояния между соседними ступенями пифагорова строя неодинаковы. Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад (не случайно в таблице 1 на с. 107 имеется семь ладов — по одному на каждую из семи нот октавы). Поэтому, чтобы сыграть мелодию в лидийском ладу от другой ноты (чего, безусловно, требовали ограниченные возможности человеческого голоса: один поет выше, другой — ниже), лиру также следовало перестраивать. (Конечно, если всю жизнь играть в одном ладу и одной тональности, то семи нот в октаве будет вполне достаточно. До сих пор прекрасно обходятся семью звуками некоторые гармошки и другие народные инструменты.)

Итак, для того, чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т. е. иметь одинаковые высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон-интервал пополам на два полутона, т. е. получить еще пять дополнительных звуков, и шкала пифагорова строя станет равномерной. Но вот тут-то и таилась основная трудность.

Дело в том, что половина тона 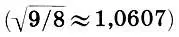в точности не равна полутону (256/243≈1,0545) (см. с. 105). Поэтому если в качестве единого масштаба строя взять полутон 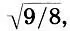т е заменить на него имеющиеся в (8.1) два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву (2), а чуточку выше: 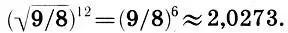Интервал между октавой, полученной шагами по 12-равномерным полутонам 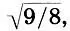и чистой октавой равен (9/8) 6:2 ≈ 1,0136 и называется пифагоровой коммой *.