Александр Волошинов - Математика и искусство

Представляя пифагорову комму в виде

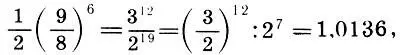
мы получим еще один важный результат: 12 квинт с точностью до пифагоровой коммы равны 7 октавам .

Но 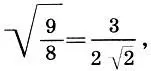т. е. новый полутон содержал иррациональное число 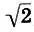, которого пифагорейцы боялись как огня. Взять столь "некрасивое" число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путем: в качестве основы музыкальной гаммы они взяли квинту, "красивое" число 3/2.

* (Коммой (от греч. komma — отрезок) в музыкальной акустике называется интервал, не превышающий 1/9 целого тона. Пифагорова комма приблизительно равна 1/9 тона . )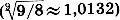

Рассмотрим ряд, составленный из степеней числа 3/2:

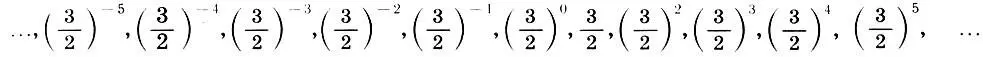
Оказывается, с помощью этого красивого симметричного ряда можно получить все интервальные коэффициенты пифагорова строя. Начнем с середины ряда 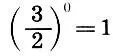и все получаемые звуки будем сводить в одну октаву, умножая или деля их интервальные коэффициенты на нужные степени числа 2 (интервальный коэффициент октавы). Новые звуки будем обозначать либо ближайшим снизу основным звуком с добавлением слова "диез" при движении по квинтам вверх, либо ближайшим сверху основным звуком с добавлением слова "бемоль" при движении по квинтам вниз. Это означает соответственно повышение или понижение основного звука. Итак,

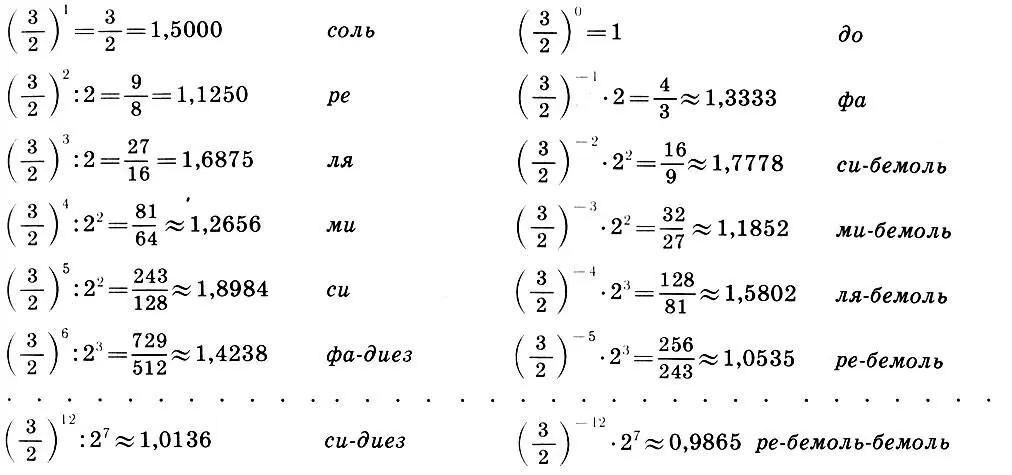(8.2)

Как видим, двигаясь по квинтам вверх и вниз от основного тона, мы получили все ступени пифагорова строя (8.1), каждая из которых в свою очередь может быть повышена, понижена, дважды повышена или понижена и т. д. Процесс этот, к сожалению, бесконечен. Точного октавного повторения основного тона ( до ) мы так и не получим. (Легко видеть, что си-диез и ре-бемоль-бемоль совпадают с основным тоном ( до ) опять же с точностью до пифагоровой коммы.) Следовательно, и точно разделить октаву на целое число частей этим методом мы не сможем.

Таким образом, желая разделить пять тонов в (8.1) на полутона, мы получили, по крайней мере, 10 промежуточных звуков. Новый пифагоров строй примет вид (интервальные коэффициенты новых звуков для краткости опущены)

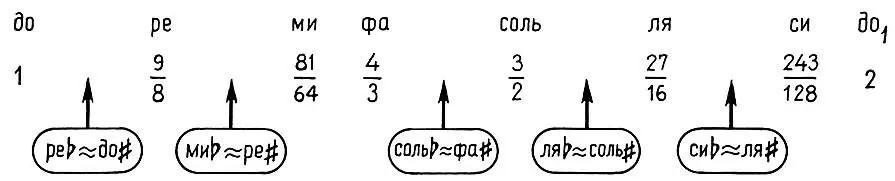
Какие из этих дополнительных звуков взять: с бемолями или диезами? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то "волшебное пение" скрипки, которое доступно только ей одной *.

*( Каким тонким является инструмент скрипка, убеждает простой пример из книги известного венгерского скрипача Карла Флеша "Искусство скрипичной игры": "Пусть на струне ля необходимо сыграть два звука ля и си-бемоль второй октавы. Разница между этими звуками равна 60 Гц. Расстояние на грифе — 2 мм, следовательно, на одно колебание струны приходится 1/30 мм. Предполагая, что ля взято чисто, и желая сыграть математически чисто си-бемоль, мы должны поставить палец в нужное место струны с точностью до 1/30 мм". Насколько же чувствительными должны быть слух и пальцы скрипача, чтобы отмерить расстояние с точностью до 1/30 мм (это 33 микрона)! )

Что касается инструментов с фиксированной высотой звуков, то введение десяти дополнительных звуков на семь основных слишком усложнило бы и сами инструменты, и игру на них. Тем более что и это не решало окончательно проблему и более тонкие построения требовали все новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же, руководствуясь мудрым критерием простоты (и красоты), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали черными (дополнительными) клавишами фортепиано.

Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить самостоятельно), то их попросту приравняли между собой ( до-диез стал равен ре-бемолю и т. д.).

Такое приравнивание звуков с одинаковой высотой, но разными названиями в теории музыки называется энгармонизмом . Тонкости ладового звучания были принесены в жертву простоте. Инструменты же с числом звуков в октаве, превышающим 12, можно увидеть только в музеях. В московском Музее музыкальной культуры имени М. И. Глинки хранится рояль русского писателя, музыканта и музыковеда В. Ф. Одоевского (1804-1869), в каждой октаве которого имеется не 12, а 17 клавиш, настроенных согласно (8.2).

Квинтовая цепь пифагорова строя дала простой способ настройки инструментов с фиксированной высотой звуков: органов, клавесинов, фортепиано. От основного тона (сегодня по общему признанию им является звук ля первой октавы) откладывались семь октав — скелет музыкальной шкалы. Эти октавы заполнялись 12 звуками, полученными ходами по квинтам вверх и вниз. Какие из звуков взять за дополнительные — повышенные или пониженные,- особого значения не имело. Важно было другое: пифагорова комма оставалась внутри октавы . Ее можно было переместить в любое место октавы, но нельзя было сделать только одного: нельзя было от нее избавиться! И она продолжала портить кровь музыкантам на протяжении столетий. Почему?

Если взять пифагоров строй с пониженными дополнительными звуками:

то в таком строе все квинты будут звучать чисто (иметь интервальный коэффициент 3/2), кроме одной. Квинта си-соль-бемоль будет иметь интервальный коэффициент 1024/ 729: 243/ 256≈1,4798, а не 1,5! От чистой квинты она, разумеется, отличается на пифагорову комму: 1,5/1,4798≈1,0136. Такая квинта на органе издавала пронзительный, неприятный звук, похожий на завывание волка, за что и была прозвана "волчьей квинтой" или просто "волком". Обращением "волчьей квинты" является "волчья кварта" соль-бемоль-си , которая также отличается от чистой кварты (4/3 = 1,333...) на пифагорову комму: