Александр Волошинов - Математика и искусство

Прекрасное описание "этоса" греческих ладов мы находим в книге древнеримского писателя Апулея (ок. 124 — ?) "Флориды": "Жил когда-то флейтист по имени Антигенид. Сладостен был каждый звук в игре этого музыканта, все лады были знакомы ему, и он мог воссоздать для тебя, по твоему выбору, и простоту эолийского лада, и богатство ионийского, и грусть лидийского, и приподнятость фригийского, и воинственность дорийского".

Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского "серебряного века" профессор А. Ф. Лосев (1893-1988) [14] Судьба Алексея Федоровича Лосева счастлива и трагична. Счастлива, потому что до последнего дня своей 95-летней жизни Лосев сохранил поразительную работоспособность и успел завершить главный труд — восьмитомную "Историю античной эстетики". Трагична, потому что другие восемь томов его сочинений, написанных на полвека ранее (1927 — 1930), были преданы анафеме, а сам автор, будучи незаконно репрессирован, продолжил свои философские изыскания на строительстве Беломорско-Балтийского канала, откуда он писал: "Я закован в цепи, когда в душе бурлят непочатые и неистощимые силы". Одна из этих работ Лосева — "Музыка как предмет логики" — могла бы служить путеводной звездой к этой книге. И все-таки судьба А. Ф. Лосева счастлива, ибо рукописи не горят. Сегодня огромное философское наследие А. Ф. Лосева обретает свое второе рождение. : "Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. "Веселые" же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки... Так задумчива, печальна и благородна вся греческая скульптура".

Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о "сладкой лидийской мелодии" или о "разнообразной лидийской мелодии".

Таким образом, мы видим, что вопрос об "этосе" ладов не решается однозначно и во многом определяется традицией применения того или иного лада. И в наше время слушатель, воспитанный, например, на тонкой и своеобразной индийской музыке, вообще не отличит мажора от минора, не говоря уж об их "этосе". Конечно, мажорный лад отличается более светлыми и радостными тонами и тому есть объективные причины, о которых мы расскажем в главе 10. Но реализация этих возможностей зависит от массы других факторов (темп, ритм, мелодический рисунок и т. д.), и поэтому есть много веселых, энергичных произведений в миноре и грустных, задумчивых — в мажоре. Вспомним хотя бы "Патетическую сонату" до минор Бетховена, этот огненно-страстный монолог Героя, зовущего на яростную схватку и даже на смерть. Многие художники подобрали многие эпитеты к этой сонате (хотя, пожалуй, лучший из них — патетическая — принадлежит самому Бетховену), но только грустной — минорной — ее назвать никак нельзя. Напротив, Ноктюрн № 2 соч. 9 ми бемоль мажор Шопена пронизан настроением нежной мечтательности. Это подернутые дымкой грусти воспоминания автора, но отнюдь не веселая — мажорная — пьеса. В заключение попытаемся сказать несколько слов об "этосе интервалов", ибо именно анализу музыкальных интервалов и посвящена настоящая глава. Попытаемся, потому что данный вопрос еще более спорный и неразработанный, чем "этос ладов". И все-таки...

До сих пор мы ничего не говорили о "самом совершенном консонансе" — приме (унисоне) (l 2/l 1= 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость. Вспомним хотя бы бесподобную игру в унисон ансамбля скрипачей Большого театра.

Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является "Песня о Родине" композитора И. О. Дунаевского (1900-1955). В ее запеве ("От Москвы до самых до окраин...") дважды звучит восходящая октава (l 1/l 2= 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l 1/l 2= 3/2) также звучит широко, но более рельефно и динамично, чем октава.

Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l 1/l 2= 4/3), например "Интернационал", "Гимн Советского Союза", "Марсельеза". Здесь интервал кварты звучит решительно и активно, как призыв к действию.

Особый "этос" у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня "Во поле береза стояла" начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.

А наиболее неприятным и неблагозвучным является интервал тритон или полуоктава (l 1/l 2= 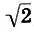). Своей неблагозвучностью этот интервал "подсказал" Архиту "музыкальное доказательство" иррациональности .

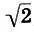Не правда ли, удивительные открытия сделали мы в этой главе? В музыкальной гамме мы обнаружили все математические пропорции, а для доказательства иррациональности 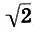использовали музыкальную гамму. Мы нашли математический скелет музыкальной гаммы и увидели, насколько тонко (задолго до нашей эры!) древние греки чувствовали музыку. Но безудержный полет фантазии увлекал античных мыслителей все дальше, в заоблачные дали, в поиски всемирной "космической музыки". И хотя поиски эти оказались бесплодными, а античная космология с современной точки зрения кажется слишком наивной, не нужно спешить смеяться над нашими предшественниками; гораздо полезнее извлечь уроки из их опыта, о чем и говорится в эпиграфе к следующей главе.