Александр Волошинов - Математика и искусство

Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит. Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.

Древние уверяли, что уже Пифагор Знал законы колебания струны монохорда и построения музыкальных созвучий (консонансов), однако запись об этих законах мы находим у пифагорейца Архита из Тарента (428-365 гг. до н. э.), жившего На полтора столетия позже Пифагора. Архит был, безусловно, самым выдающимся представителем пифагорейской школы, другом философа Платона и учителем математика Евдокса (ок. 408 — ок. 355 гг. до н. э.), государственным деятелем и полководцем. Многосторонность Архита поразительна: он решил знаменитую де-лосскую задачу об удвоении куба, заслуженно считался крупнейшим пифагорейским теоретиком музыки, первым упорядочил механику на основе математики и свел движения механизмов к геометрическим чертежам, работал над деревянной моделью летающего голубя. По мнению Ван дер Вардена, Архит является автором VIII книги "Начал" Евклида, в которой изложена арифметическая теория пропорций. Как государственный деятель Архит пользовался исключительным уважением: он семь лет подряд избирался стратегом *, хотя по закону стратеги выбирались лишь на один год. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. "Славный Архит, земель, и морей, и песков исчислитель..." — писал Гораций.

* ( Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )

"Законы Пифагора — Архита", на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:

1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:

(6.2)

здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).

2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.

Эти интервалы — "совершенные консонансы", и их интервальные коэффициенты позже получили латинские названия *:

*( Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д. )

октава

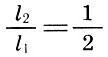
квинт

кварта

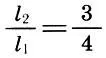
Треугольное число 10

Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида 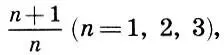тем созвучнее интервал.

"Второй закон Пифагора — Архита" и сейчас кажется удивительным. (В его истинной природе мы разберемся в главе 10.) Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной (см. гл. 7).

Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l 1, то вместе со всей струной монохорда длины l 1= 12l будут созвучны ее части длины l 2= 6l — звук на октаву выше (l 2/l 1= l/2), l 3= 9l — звук на квинту выше (l 3/l 1= 2/3) и l 4= 8l — звук на кварту выше (l 4/l 1= 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это "та гамма, по которой поют сирены". При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.

Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять , т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения. Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f 1и f 2= 2f 1, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f 3= (f 1+ f 2)/2. Но тогда длина струны l 3выразится через длины струн l 1и l 2согласно (6.2) следующим образом:

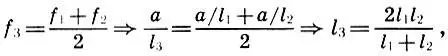
т. е. l 3есть среднее гармоническое l 1и l 2(см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f 1и f 2переходит в среднее арифметическое для длин l 1и l 2:

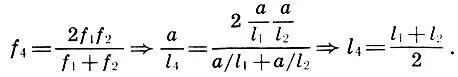
Вспоминая, что мы вместе с Архитом приходим к важному выводу:

(6.3)

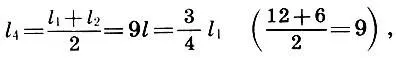(6.4)

т. е. квинта есть среднее гармоническое длин струн основного тона l 1 и октавы l 2 , а кварта — среднее арифметическое l 1 и l 2 .

Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел: