Александр Волошинов - Математика и искусство

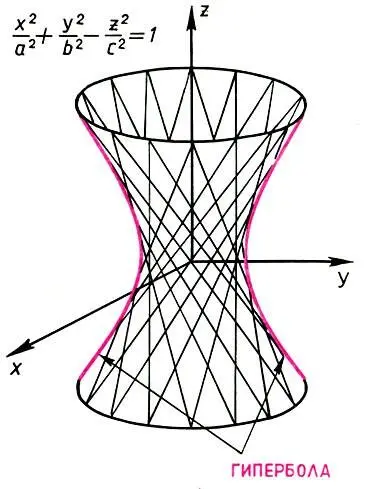
Радиобашня (впоследствии телебашня) Шухова на Шаболовке (Москва. 1922) и линейчатое свойство однополостного гиперболоида

Строительство железобетонных покрытий требовало опалубки, удерживающей жидкий бетон и придающей ему лучшую форму. Опалубку же удобнее всего делать из прямых досок. Простейшие поверхности, образованные движением прямой в пространстве и называемые линейчатыми поверхностями — цилиндры и конусы,- были известны давно. Еще древние римляне сооружали цилиндрические своды. А существуют ли другие линейчатые поверхности? Ответ на этот вопрос архитекторам подсказали математики, которые обнаружили еще два типа линейчатых поверхностей:

однополостный гиперболоид:

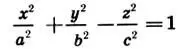(13.1)

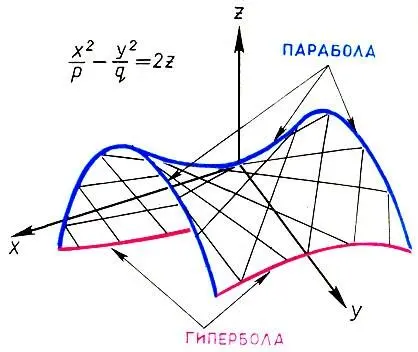
гиперболический параболоид:

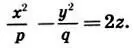(13.2)

Канонические уравнения этих поверхностей (13.1) и (13.2) легко представить в виде

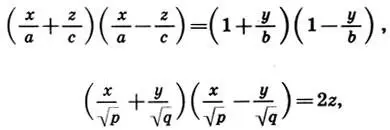
откуда и видно, что они образованы двумя семействами прямых в пространстве (в уравнение прямой переменные х, у, z входят только в первых степенях).

Архитекторы воспользовались открытием математиков. Форму однополостного гиперболоида имеют градирни — устройства для охлаждения воды атмосферным воздухом. Линейчатое свойство однополостного гиперболоида положено в основу конструкции Шаболовской радиобашни в Москве, построенной по проекту замечательного русского советского инженера, почетного академика В. Г. Шухова (1853- 1939). Башня Шухова состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов, причем каждая часть сделана из двух семейств прямолинейных балок, соединенных в точках пересечения.

Если однополостный гиперболоид отдает должное "пользе" в архитектуре, то гиперболический параболоид (архитекторы называют его красивым сокращенным именем гипар) благодаря своей выразительной и элегантной форме служит "красоте". Архитектурные возможности гипаров открыл инженер Феликс Кандела — испанский патриот, сражавшийся против фашистской диктатуры Франко, в 1939 г. вынужденный эмигрировать в Мексику. Кандела с блеском продемонстрировал выразительные свойства гипаров на различных сооружениях — от промышленных зданий до ресторанов, ночных клубов и церквей. Объединяло столь функционально несхожие сооружения одно: в них математическая поверхность становилась произведением архитектурного искусства. Линейчатое свойство гипаров позволяет разрезать их по прямолинейным образующим и составлять из нескольких гипаров экзотические конструкции. Именно так поступил в 1958 г. Ле Корбюзье, построив причудливый павильон фирмы "Филипс" на Международной выставке в Брюсселе.

Точно сказал о внутренней красоте гипаров один из ее приверженцев — американский инженер Вейдлингер: "Красота форм достигается не средствами "косметики", а вытекает из сущности конструкции. Сама по себе форма является почти эпюрой [24] Эпюра (от франц. epure — чертеж) — гРафик закона изменения некоторой величины. усилий, которые она должна воспринять". А для людей, которые видят только внешнюю красоту гипаров, они напоминают крылья огромных фантастических птиц, опустившихся на нашу Землю лишь отдохнуть и в каждое мгновение готовых взмахнуть крыльями-гипарами и улететь в свои неведомые миры. Именно эта "вторая реальность", "поэтическое дыхание" и преобразуют математическую поверхность, строительную конструкцию в искусство, именуемое архитектурой.

Ни один из видов искусств так тесно не связан с геометрией, как архитектура. "Окружающий нас мир — это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг — геометрия. Никогда мы не видим так ясно таких форм, как круг, прямоугольник, угол, цилиндр, гипар, выполненных с такой тщательностью и так уверенно". Эти восторженные слова о геометрии принадлежат Ле Корбюзье.

Вечерний зал в Акапулько (Мексика) архитектора Канде-ла и линейчатое свойство гиперболического параболоида

Но в отличие от "абстрактной", "математической" геометрии "архитектурная" геометрия наполнена собственным эстетическим содержанием. Дело в том, что образы "математической" геометрии бестелесны: они не имеют толщины, не имеют веса и потому свободно парят в нашем воображении. Иное дело — образы "архитектурной" геометрии. Они созданы из конкретного материала: они весомы, они живут в поле земного тяготения. Геометрическую фигуру, например пирамиду, мы можем поворачивать в нашем воображении в любую сторону — от этого ее свойства не изменяются. Но попробуйте мысленно повернуть вершиной вниз пирамиду Хеопса, и вам сразу станет не по себе: пирамида начнет качаться из стороны в сторону и разваливаться на куски. Причина здесь очевидна: на пирамиду Хеопса даже в нашем воображении действует земное притяжение. И для того чтобы обеспечить своему сооружению бессмертие, древнеегипетский зодчий гениально воплотил в каменной пирамиде важнейшее правило устойчивости и прочности конструкции — расширение книзу. Так пирамида в архитектуре закономерно стала олицетворением устойчивости и прочности, вечности и покоя. В этом ее эстетическое содержание. Художественное выражение закономерностей архитектурного сооружения или конструкции называется архитектоникой или просто тектоникой. Можно сказать, что пирамида является символом тектоники всей классической архитектуры, ее эстетическим флагом.

Современное зодчество бросило вызов классической тектонике. Получив в свое распоряжение особо прочные материалы и конструкции, оно стремится перевернуть вверх ногами "пирамиду архитектоники". Современная архитектура, будто преодолев силы тяготения, парит в воздухе. Человечество всегда мечтало о легкой и воздушной архитектуре, и вот в XX веке эти мечты обретают плоть. Горизонтальные плоскости, будто летящие в пространстве ("Дом над водопадом" в Бер-Ране, США, арх. Ф. Райт, 1936 г.); гигантские нависающие объемы (Клуб им. И. В. Русакова в Москве, арх. К. Мельников, 1929 г.); V-образные опоры, оторвавшие здание от земли ("Лучезарный дом" в Марселе, арх. Ле Корбюзье, 1952 г.); стены, превращенные в витражи, в которые любуются золотые купола Кремлевских соборов (Кремлевский Дворец съездов, арх. М. Посохин и др., 1961 г.); причудливые линии козырьков и сводов-оболочек в форме гипаров (церковь де ла Виргин Милагроза в Мехико, инж. Ф. Кандела, 1955 г.)- все это приметы современной архитектоники и ставшие классикой примеры современной архитектуры. Все эти приметы, собранные вместе, легко обнаружить в здании Штаб-квартиры ЮНЕСКО в Париже (арх. П. Нерви и др., 1957 г.), которое и было задумано как символ современной архитектуры.