Александр Волошинов - Математика и искусство

Почему художник не довольствовался трехмерной скульптурой, а стремился к двумерному изображению оригинала, понять нетрудно: плоская поверхность пещеры или стены храма, глиняной таблички или папируса, пергамена или бумаги была удобным носителем графической информации. В последних случаях такую поверхность можно было попросту свернуть в рулон и унести с собой.

Люди издревле научились отображать всевозможные объекты окружающего их трехмерного мира на двумерную плоскость картины. Однако по мере развития такого искусства отображения все чаще возникал вопрос: насколько точно и насколько убедительно эти плоские образы отражают реальные трехмерные прообразы? На эти вопросы призвана была ответить наука, и прежде всего геометрия. И она по мере сил отвечала на них, хотя решение столь простой на первый взгляд задачи растянулось на тысячелетия.

В этой главе мы рассмотрим с точки зрения геометрии, какие основные возможности имеются в решении задачи отображения трехмерного пространства на двумерную плоскость. А в главе 22 мы увидим, как эти возможности реализовы-вались в искусстве живописи.

Раздел геометрии, в котором изучаются различные методы изображения пространственных форм на плоскости, называется начертательной геометрией . В основе начертательной геометрии лежит метод проекций , сущность которого такова. В пространстве выбирают фиксированную точку S — центр проектирования и плоскость проекций К ( картинную плоскость ), не проходящую через S. Для получения изображения — проекции [32] Проекция (лат. projectio) — бросание вперед. — объекта на плоскость К через центр проекций S и каждую точку А, В, С,... объекта проводят проектирующие лучи до пересечения с плоскостью К. Совокупность точек пересечения проектирующих лучей с картинной плоскостью и даст изображение (проекцию) объекта, которое называют центральной проекцией .

Представим теперь, что центр проектирования S уходит в бесконечность. Тогда проектирующие лучи становятся параллельными между собой. Считая центр проектирования расположенным в бесконечно удаленной точке S ∞, мы, таким образом, приходим к важному частному случаю центрального проектирования — параллельному проектированию . Наконец, важным частным случаем параллельных проекций являются ортогональные проекции , когда проектирующие лучи ортогональны К, т. е. образуют прямые углы с плоскостью проекций К.

При построении проекций некоторые свойства оригинала сохраняются и на его проекции. Такими неизменными свойствами — инвариантами — при центральном проектировании обладают:

1) точки (проекция точки — точка);

2) прямые;

3) свойство точки принадлежать прямой.

При параллельном проектировании помимо того сохраняются следующие свойства:

4) параллельность прямых;

5) отношение отрезков прямых;

6) метрические свойства плоских фигур, параллельных картинной плоскости (плоские фигуры, параллельные картинной плоскости, проектируются на эту плоскость без искажений).

Обратим внимание на то, что свойство параллельности прямых при центральном проектировании не сохраняется.

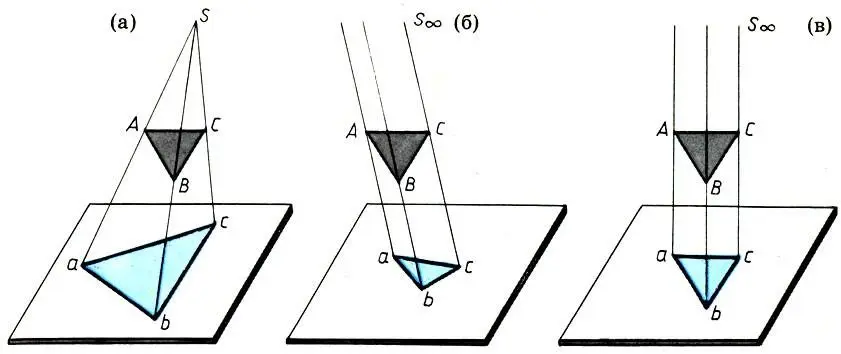
Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в)

Приложение начертательной геометрии к технике выдвинуло требование "обратимости" чертежа, т. е. возможности точного определения пространственной фигуры по плоскому чертежу, или, говоря языком математики, взаимно однозначности отображения пространства на плоскость. Рассмотренные проекции являются однозначными, но не взаимно однозначными отображениями, т. е. каждой точке пространства соответствует единственная точка плоскости, но не наоборот. Нетрудно убедиться и в том, что для определения положения точки в пространстве по ее чертежу необходимо иметь две проекции точки, полученные из двух центров или при двух направлениях проектирования. Эта гениально простая мысль и составляет основу начертательной геометрии, заложенную выдающимся французским математиком, активным деятелем Великой французской революции, другом и советником Наполеона Гаспаром Монжем (1746-1818).

Суть метода Монжа можно изложить двумя предложениями, как это сделал член-корреспондент АН СССР Б. Н. Делоне: "Пространственный объект проектируется ортогонально (т. е. перпендикулярами) на плоскость и также проектируется на некоторую другую ей перпендикулярную плоскость, и затем одна из этих плоскостей поворачивается вокруг прямой пересечения этих плоскостей, пока не совместится с другой. В результате на одной и той же плоскости оказываются две различные проекции (вида) рассматриваемого объекта, по которым уже можно, методами Монжа, восстановить размеры, углы и т. д., имеющиеся у данного пространственного объекта в натуре."

Несмотря на то что ортогональные проекции известны человечеству с незапамятных времен (вся живопись Древнего Египта есть не что иное, как ортогональные проекции на плоскость рисунка), простая мысль использовать две ортогональные проекции для получения взаимно однозначного отображения пространства на плоскость пришла Монжу лишь в конце XVIII века. Имея огромное практическое значение в теории фортификации, метод Монжа еще в течение 15 лет оберегался как военная тайна. Простота метода Монжа ошеломила современников. Познакомившись с его идеями, Лагранж, перемежая иронию с восторгом, воскликнул: "До слушания лекции Монжа я не знал, что мне известна начертательная геометрия!"

На рисунке показаны различные типы проекции одного и того же прямоугольного параллелепипеда с отношением сторон 1:2:3. Метод ортогональных проекций Монжа иллюстрирует рисунок а. Заметим, что третья проекция с точки зрения математики является лишней, но ею часто пользуются, чтобы создать более полное представление о пространственном теле. Как отмечалось, при ортогональном проектировании сохраняются истинные размеры контуров тела.

Однако ортогональные проекции не дают целостного впечатления о форме пространственного объекта. Более наглядное представление о форме тела дают аксонометрические проекции [33] Аксонометрия — от греч. axon — ось и metreо — измеряю. — частный вид параллельных проекций, отображающих на плоскость К все точки пространственного объекта вместе с декартовой системой координат, к которой этот объект отнесен. На рисунке б построена аксонометрическая проекция нашего параллелепипеда. Мы видим, что в аксонометрии происходят искажения линейных размеров, различные по разным осям. Согласно основной теореме аксонометрии — теореме Польке, три произвольных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из некоторой точки пространства, Следовательно, аксонометрические оси и коэффициенты искажения по ним (отношение длины по аксонометрической оси к истинной длине по соответствующей оси) могут быть выбраны произвольно. (В нашей аксонометрии углы между осями равны 120°, а коэффициенты искажения — 1.)