Александр Волошинов - Математика и искусство

Итак, построения рисунка дают нам не только ряд золотого сечения (19.2), но и гамму геометрических прогрессий вида

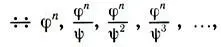(19.4)

соответствующие члены которых также находятся в золотой пропорции.

Любопытно, что в 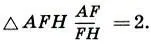Заметим также, что в

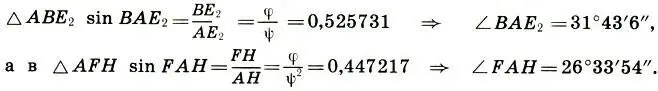
Таким образом, меньшие углы в треугольниках ΔВЕ 2и AFH почти равны ; следовательно, эти треугольники почти подобны , а углы исходного квадрата делятся "диагоналями" почти точно на три части . Итак рассмотренное построение дает нам прекрасный пример приблизительной симметрии (см. гл. 4).

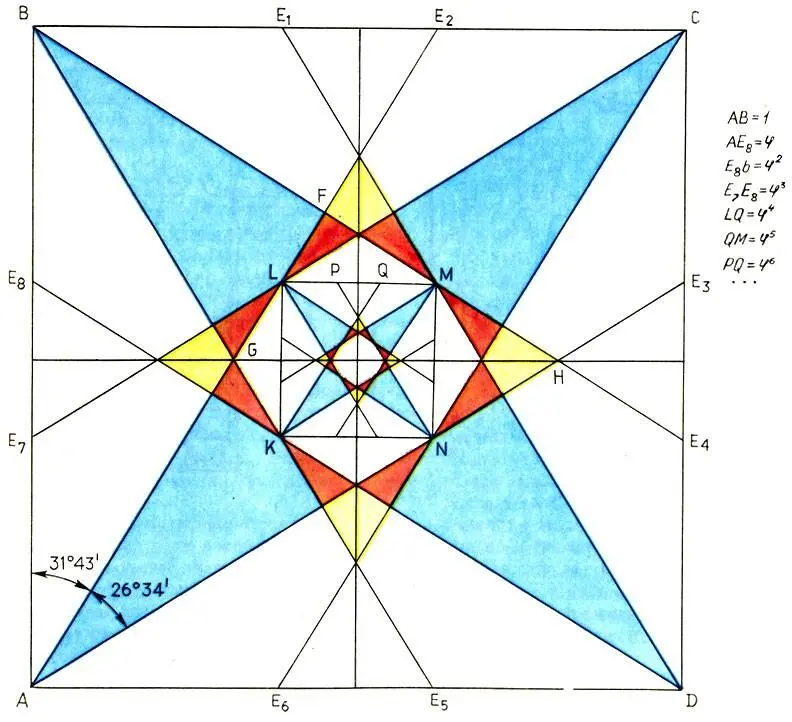
Созвездие восьмиконечных звезд, вписанных в квадрат, содержит целую гамму золотых пропорций и использовалось древнеегипетскими художниками в пропорциях человека

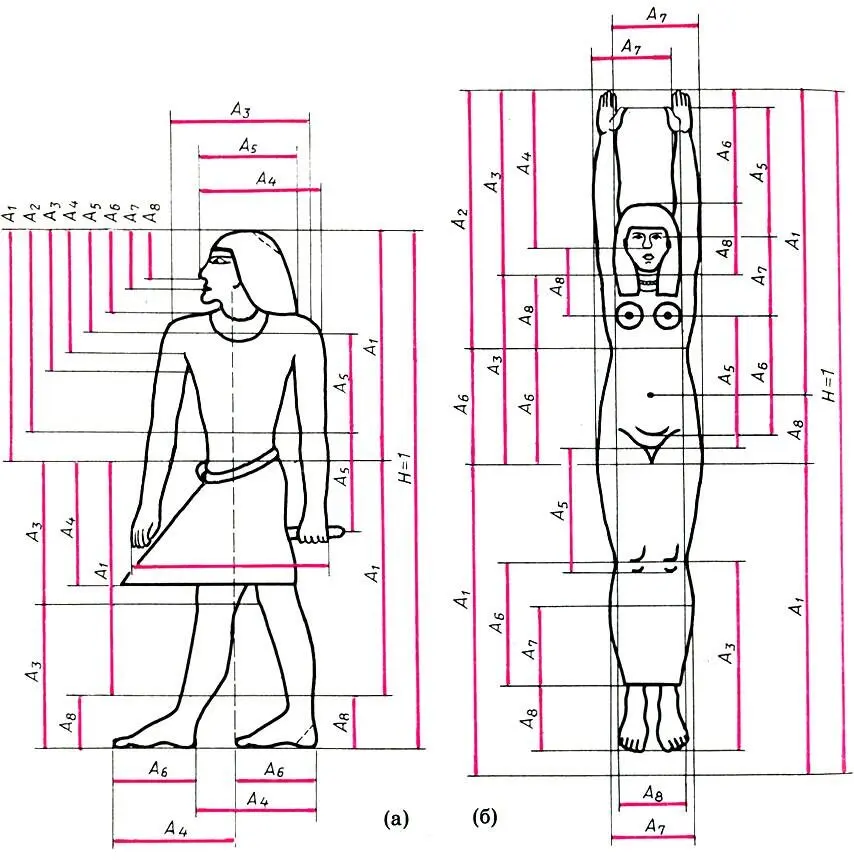
Математическое построение древнеегипетских рисунков на базе восьми пропорциональных величин (по Ф. де Кора). Фигурки жреца (а) и богини Ночи (б)

Интересно, что... Впрочем, достаточно. Оставим радость открытия любителям математики, тем более что у любителей искусства, видимо, давно уже созрел вопрос: "А какое отношение вся эта геометрия и алгебра имеют к теме нашего разговора — пропорциям человека?" А вот какое.

По мнению французского египтолога Фурнье де Кора, восемь величин из ряда (19.4), а именно

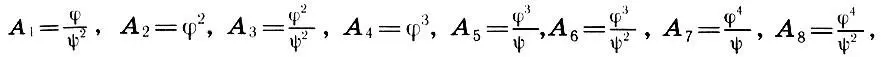(19.5)

определяют весь пропорциональный строй древнеегипетской живописи. Этот вывод де Кора основан на кропотливом изучении пропорции многих памятников изобразительного искусства Древнего Египта. На рисунке мы видим, что местоположение всех основных элементов фигур — уровень глаз, носа, рта, шеи, плеч, пояса и т. д.- с удивительной точностью определяется пропорциональными величинами (19.5), умноженными на общую длину фигурки (Н). Пользуясь (19.5) и соотношениями φ n= φ n+1+ φ n+2, легко доказать равенства типа 2А 1+ А 8= 1, А 1+ А 2+ А 6= 1, А 1+ 2А 3= 1, А 6+ А 8= А 3, А 3+ A 8= A 2, А 3+ А 6= А 1, и т. д.

Конечно, ряд (19.4) дает настолько богатую гамму пропорций, что при достаточном числе членов она может быть точнее миллиметровой линейки. Математику, разумеется, не понравится, что в (19.5) пропущены члены φ, φ/ ψ, φ2/ ψи φ 4отчего теория де Кора теряет в логической стройности. Да, по прошествии четырех тысячелетий трудно установить, какой именно системой пропорций пользовался древнеегипетский художник. Поэтому так много различных теорий пропорций. Но бесспорно другое: древнеегипетский художник применял жестко детерминированную систему математических правил, которая на века определила стиль древнеегипетского изобразительного искусства. Эта математика рисунка, ставшая каноном, на века сковала искусство Древнего Египта.

Описание египетского канона позднего периода и любопытную историю, связанную с ним, мы находим у древнегреческого историка Диодора Сицилийского (ок. 90-21 гг. до н. э.). По преданию, отец Пифагора Мнесарх построил на родном острове Самос храм в честь Аполлона Пифийского, статую для которого поручили изваять прославленным греческим скульпторам. "Из древних скульпторов наибольшею славою пользовались у них Телекл и Феодор, сыновья Река, которые соорудили для самосцев статую Аполлона Пифийского. Рассказывают, что одна половина этой статуи была приготовлена Телеклом на Самосе, другая же часть была сделана его братом Феодором в Эфесе. Будучи сложенными, эти части настолько соответствовали одна другой, что казалось, будто все произведение исполнено одним мастером. Однако этот род работы никогда не применяется у греков, но большей частью употребляется у египтян... У них соразмерность статуи определяется не на глаз, но они после того, как высекут камни и обработают, разделив их на части, берут пропорцию от мельчайших до наибольших частей; рост тела они делят на 21 1/ 4— часть и так дают все соразмерности живого человека. Поэтому после того, как работники сговорятся о размерах, то, разделивши между собой труд, обрабатывают согласно заданной величине так точно, что работа их наполняет изумлением". Возможно, что эта история, рассказанная Диодором, не более чем легенда. Но важен в ней даже не факт совпадения сложенных изваяний, сколько сама постановка такого вопроса. В этой истории, даже если она и легенда, отражена безграничная вера древних греков в могущество математики, которую с равным успехом можно применять не только в инженерных расчетах (вспомним о самосском туннеле, с. 89), но и в искусстве ваяния. Создавая свои бессмертные творения, древние не боялись "алгеброй разрушить гармонию" и твердо верили: математика поможет там, где, по словам Дюрера, "рука из-за спешки обманет тебя".

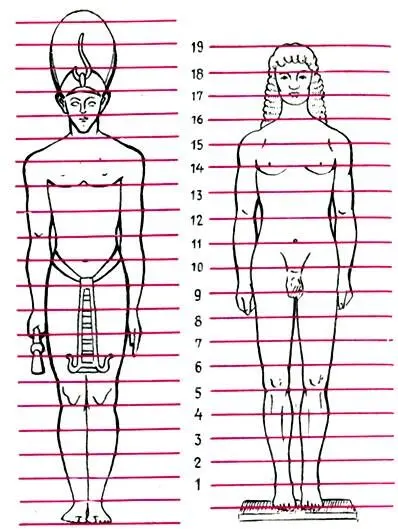
Курос из Теней ('Аполлон Тенейский'). Ок. 560 до н. э. Тождественность пропорций Аполлона Тенейского и египетского канона ваяния позднего периода еще раз доказывает факт влияния древнеегипетского искусства на раннее греческое искусство периода архаики

На рисунке изображен египетский канон, описанный у Диодора. Высота фигуры разделена точно на 21 — части, причем одно целое деление соответствует длине среднего пальца. Высота фигуры без головного убора составляет 19 частей. Рядом расположена греческая скульптура Аполлона Тенейского, относящаяся к середине VI века до н. э.- так называемому архаическому (от греч. "архайос" — древний) периоду греческого искусства. Точное совпадение пропорций этих двух фигур является математическим доказательством достаточно очевидной истины: греческое искусство периода архаики взросло на почве древнеегипетского искусства. Конечно, художественные образы этих фигур совершенно различны. Аполлон Тенейский, юноша-атлет (курос), светится жизнью и радостью: еще мгновение — и он сойдет с места навстречу новому искусству Эллады. Однако его пропорции- "математика Аполлона" — полностью сохраняют влияние древнеегипетского канона.

Греческое искусство развивалось очень динамично. Уже через 100 лет после Аполлона Тенейского, в середине V века до н. э., греческая цивилизация достигает своего апогея. Наступает период наивысшего расцвета искусства Древней Греции, именуемый периодом высокой классики. Возвышенные идеалы классики, вера в духовное, нравственное и физическое совершенство свободного эллина нашли отражение в скульптурах Поликлета, творившего во второй половине V века. Поликлет был не только гениальным скульптором, автором "Дорифора", "Дуадумена" и "Раненой амазонки", но и выдающимся теоретиком искусства.