Александр Волошинов - Математика и искусство

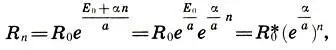
т. е. сила раздражения R nдолжна нарастать в геометрической прогрессии со знаменателем q = e α/ a.

Но ведь и гамма равномерно-темперированного строя (9.1), и ряд золотого сечения (15.4) или (15.5), и красная (17.2) и синяя (17.3) шкалы модулора Ле Корбюзье являются геометрическими прогрессиями! Следовательно, все эти "раздражители"- наших органов чувств обеспечивают равномерное возрастание (или убывание) наших ощущений. Таким образом, именно закон Вебера — Фехнера, скорее всего, и является тем математическим законом, который лежит в основе основ как музыки (музыкальная гамма), так и архитектуры (шкала пропорциональностей), той "математикой", которая связывает и музыку, и архитектуру!

Подтверждением этому могли бы стать экспериментальные значения коэффициента α/ а, полученные в результате психофизических опытов. Поскольку для равномерно-темперированной гаммы q = = 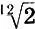= 1,06, а для ряда золотого сечения q = 1,618 (q = e α/a), то легко находим: для музыкальной гаммы α/а = 0,058, а для ряда золотого сечения α/а = 0,482. Если эти значения совпадут с экспериментальными, то это и будет хотя бы в первом приближении объяснением, почему именно 12-ступенная гамма и золотое сечение в течение тысячелетий продолжают радовать наши слух, глаз и разум.

Насколько это справедливо, покажут будущие исследования. Хочется верить, что законы красоты все-таки будут разгаданы, и, памятуя традиции Баха и Моцарта (см. с. 149), закончить последнюю главу об архитектуре и музыке мажорным аккордом.

"Ну это уж слишком! — рассердится уставший читатель.- Да, архитектура — наполовину наука, наполовину искусство, и потому "математическое начало" в ней естественно. Да, музыка слагается из колебаний среды и, следовательно, подчиняется законам акустики, которая полностью математизирована. Но какая математика нужна художнику, которому, кроме холста и красок, вообще ничего не нужно!? Примером "математики в живописи" может служить разве что картина Богданова-Бельского "Устный счет"!"

В этой части книги мы попытаемся убедить сердитого читателя в том, что он глубоко не прав.

Раздел называется "Математика и живопись", хотя, быть может, правильнее его следовало бы назвать "Математика и изобразительные искусства". Последние, как известно, объединяют живопись, скульптуру и графику. Тем не менее речь в этом разделе пойдет прежде всего о живописи: с одной стороны, потому, что живопись является ведущей составляющей изобразительного искусства, а с другой — потому, что именно в живописи заключены основные математические проблемы изобразительного искусства.

К сожалению, говоря о живописи, мы оставим в стороне ее основное изобразительное средство — цвет. Причин тому две: во-первых, ограниченные размеры книги, а во-вторых, сложность проблемы. Вопрос о цветовой гамме — совокупности взаимосвязанных цветов и их оттенков, "эстетике цвета" и "математике цвета" — во многом остается загадочным. Между тем еще Ньютон, разложивший солнечный свет на семь цветовых составляющих, заметил, что частоты v границ цветов солнечного спектра относятся как частоты самой симметричной фригийской гаммы чистого строя (8.8):

Тем самым вместе с дисперсией света Ньютон открыл и удивительную аналогию между цветом и музыкой, послужившую толчком к развитию цветомузыки. В наше время с изобретением цветного телевидения бурное развитие получила наука о количественном измерении цвета — колориметрия . Однако все эти вопросы для нас останутся в стороне.

Н. Богданов-Бельский. Устный счет. 1895. На картине изображен известный педагог, профессор С. А. Рачинский, сменивший университетскую кафедру на место учителя в сельской школе

Остановимся на другом важнейшем изобразительном средстве живописи — рисунке , который, по словам Вазари, является "отцом живописи". Рисунок играет важнейшую роль в определении очертаний предметов, их форм, объемов и взаимного расположения в пространстве. Таким образом, рисунок является "скелетом живописи", ее конструктивной основой и именно в нем заложены геометрические законы живописи. Вот почему все, что мы будем говорить о "математическом содержании живописи", будет как частный случай относиться и к графике — "одноцветной живописи", а в той части, где речь будет идти о пропорциях,- и к скульптуре. Заметим, что в скульптуре, основанной на принципе объемного трехмерного изображения предмета, само собой отпадает основная математическая проблема живописи — проблема изображения трехмерного пространства на двумерной плоскости картины, проблема перспективы.

Говоря о живописи, мы не будем касаться и таких средств языка живописи, как сюжет, композиция, колорит, светотень, контраст, фактура, тон, валёр, рефлекс, лессировка и т. д. Список этот можно продолжить: он говорит лишь о неисчерпаемых возможностях художественного образа. Однако, сколько бы мы ни продолжали этот список, сколько бы ни уточняли и ни утончали его составляющие, он не поможет нам понять закономерности языка живописи, раскрыть логику взаимосвязи и характер "содружества" тех или иных выразительных средств. Логика живописного произведения откроется нам лишь в том случае, если мы освободимся от частностей, вычленим лишь самую суть, предельно абстрагируемся, и как вершина такой абстракции встанет перед нами геометрия живописи.

Во вступлении ко второй части (с. 88) мы говорили о том, что поиски математических закономерностей в области изобразительных искусств имеют едва ли не древнейшую традицию. Блестящим тому подтверждением служит знаменитый канон Имхотепа, жившего в Древнем Египте в XXVIII веке до н. э., т. е. более чем за 2000 лет до того, как Пифагор открыл законы целочисленных отношений в музыке. Однако в отличие от объективных "законов Пифагора в музыке", которые справедливы и сегодня, "законы Имхотепа в ваянии" субъективны, и потому на смену им приходили столь же субъективные каноны Поликлета, Лисиппа и др. Тем не менее все эти каноны были попыткой найти объективные математические закономерности в строении человека — "законы красоты" человека.