Александр Волошинов - Математика и искусство

Другой важнейшей математической темой в живописи, которая также на протяжении тысячелетий стимулировала поиски и дарила находки как художникам, так и ученым, является проблема построения перспективы. Эти две темы и составят предмет последней части книги.

Во все времена, от наскальной живописи в Сахаре до полотен Сальвадора Дали, человек был и остается главной темой изобразительного искусства. "Виллендорфская Венера" или Венера Милосская, царь Хаммурапи или бог Аполлон, Сикстинская мадонна или девушка с персиками — для художника все они прежде всего были образами человека. Более того, в предыдущей части мы увидели, что образ человека, его пропорции нашли воплощение и в архитектурных произведениях от античных й древнерусских храмов до ультрасовременных сооружений Ле Корбюзье. Настало время подробнее поговорить об этих пропорциях — "законах красоты" человека [30] Конечно, каковы они, "законы красоты" человека, никто не знает; поэтому речь в этой главе пойдет лишь о пропорциях человека, которые, безусловно, являются составной частью этих законов. .

С древнейших времен пропорции человека составляли предмет изучения художника, его "математическую лабораторию". На первых порах художником руководило, быть может, не столько стремление "дойти до самой сути", сколько необходимость в каких-то объективных — числовых или геометрических — формах передать свой опыт и свое мировоззрение преемникам. Так в искусстве возникали каноны.

Известны три древнеегипетских канона : первый канон эпохи Древнего царства, приписываемый Имхотепу (XXVIII в. до н. э.), слагает рост человека из 6 ступеней ноги; второй — эпохи Среднего и Нового царства (XXI-XII вв. до н. э.) разбивает каждую ступню еще на три части и таким образом составляет рост человека из 18 единиц; третий канон позднего периода [31] Распределение канонов по периодам истории Древнего Египта весьма условно. (XI-IV вв. до н. э.) складывает рост человека из 21 части с четвертью. Текст египетских канонов не сохранился, хотя в дошедшем до нас каталоге храмовой библиотеки в Эдфу под шестым номером значится трактат "Предписание для стенной живописи и канон пропорций". Легко видеть, как с течением времени усложнялся древнеегипетский канон, хотя и на такие ничтожные для современника "уточнения" потребовалось ни много ни мало 2500 лет!

Да, мерно, как воды Нила, текло время в Древнем Египте. И столь же неторопливым, статичным было египетское искусство. Более того, следование раз и навсегда принятым канонам, в том числе и художественным, неизменность всего сущего были своего рода философией древнеегипетского общества. И эта философия оцепенения мастерски воплощена древним художником в камне. Впрочем, для нас важно другое: почти за 3000 лет до н. э. изобразительное искусство подверглось математическому анализу и анализ этот был весьма объективен, коль скоро он устраивал древнеегипетских художников на протяжении тысячелетий. Только в математических закономерностях и можно было на века сохранить художественные каноны.

Вера египтян в универсальность математического знания отражена в одном из математических папирусов, который начинается словами: "Точное сложение — врата в знание всех вещей и мрачных тайн". А вера в универсальность канона доходила до того, что один и тот же канон египтяне применяли как в живописи, так и в архитектуре. Сетка квадратов, применявшаяся с равным успехом и в ваянии, и в зодчестве, была у египтян математической основой, организующей изображение. Меняться могли лишь абсолютные размеры этой сетки, само же изображение, его пропорции оставались неизменными.

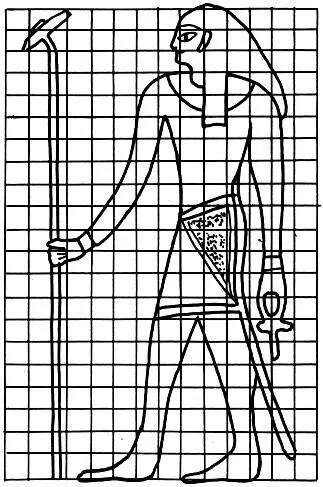
Сетка квадратов 21 1/ 4X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве

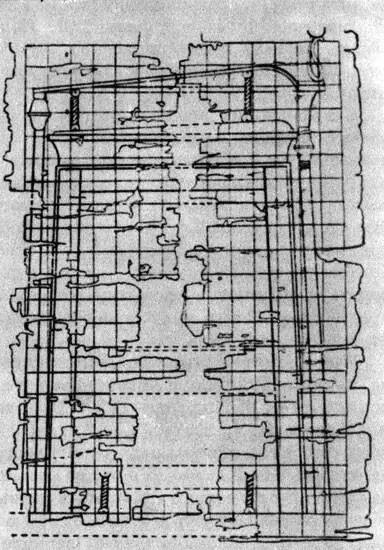
Сетка квадратов 21 1/ 4X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве

Но и внутри сетки положение фигуры строго регламентировалось математическими законами. Рассмотрим одно геометрическое построение, которое, как полагают, было известно древним египтянам. Стороны квадрата ABCD разделим в золотой пропорции точками Е i(i = 1, 2,..., 8). (Это легко сделать, разбив данный квадрат на четыре квадрата и в каждом двойном квадрате выполнив построения, указанные на рисунке, с. 265.) Из вершины квадрата проведем в точки деления по две "диагонали". В результате образуется восьмиконечная звезда, внутри которой заключены два малых квадрата, образующих звездчатый восьмиугольник. Соединяя через одну точки пересечения малых квадратов, построим меньший квадрат со сторонами, параллельными сторонам исходного квадрата. В последнем квадрате всю процедуру можно повторить. Таким образом, получится созвездие вписанных друг в друга восьмиконечных звезд, столь же красивое, как и созвездия пятиконечных и десятиконечных звезд, которые мы наблюдали на рисунках (с. 206).

Не будем перегружать рисунок дополнительными построениями и лишать любителей математики удовольствия самим найти на чертеже две гаммы треугольников, подобных прямоугольным треугольникам АВЕ 2и AFH. Отметим лишь, принимая сторону исходного квадрата за единицу, главное. В ΔАВЕ 2АВ = 1, BЕ 2= φ, АЕ 2= √1 + φ 2= ψ. В ΔABF ~ ΔАВЕ 2

AF = 1/ ψ,BF = φ/ ψ, AB = 1. Из ΔABF и ΔBFG, имеющих общую сторону BF, можно найти элементы ΔBFG: BF = φ/ ψ, FG = φ/ 2ψ,BG = ψ/ 2, а значит, и элементы ΔAFH: AF = 1/ ψ, FH = 1/ 2ψ, АH = ψ/ 2φ. (Напомним, что φ = (√5 — 1)/2 и при выводе соотношений в треугольниках используется аддитивное свойство ряда золотого сечения: 1 = φ + φ 2, φ = φ 2+ φ 3, ... .)

Продолжая рассмотрение подобных треугольников, легко увидеть, что отношения соответствующих элементов треугольников, подобных ΔABE 2, образуют бесконечно убывающую геометрическую прогрессию :

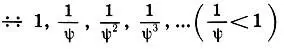(19.1)

а отношения соответствующих элементов треугольников, подобных ΔAFH, образуют прогрессию:

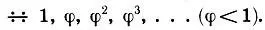(19.2)

Кроме того, имеют место комбинации двух основных типов прогрессий, а именно прогрессии вида

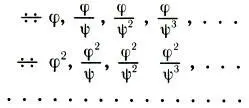(19.3)