Джо Боулер - Математическое мышление

Много лет школьная дисциплина теряла связь с наукой, которую используют ученые, и с математической жизнью. Ученики тратили тысячи часов на изучение процедур и правил, которые им никогда не пригодятся. Конрад Вольфрам — директор Wolfram-Alpha, одной из важнейших математических компаний во всем мире — резко критикует традиционный подход к преподаванию математики и категорически заявляет, что суть ее не сводится к вычислениям. В своем выступлении на конференции TED [10], которое посмотрели более миллиона людей, Вольфрам предложил, чтобы занятия математикой состояли из четырех этапов.

1. Постановка вопроса.

2. Переход от реального мира к математической модели.

3. Выполнение вычислений.

4. Возврат от модели к реальному миру, чтобы определить, получен ли ответ на исходный вопрос.

Первый этап подразумевает постановку продуманного вопроса по поводу определенных данных или ситуации. Это первое математическое действие, которое необходимо выполнить на рабочем месте. В США самая востребованная профессия — аналитик, или специалист по обработке больших данных, имеющихся в распоряжении каждой компании, и постановке важных вопросов по поводу этих данных. Второй этап, о котором говорит Вольфрам, — создание модели, позволяющей найти ответ на поставленный вопрос; третий — вычисления, а четвертый — возврат от модели к реальному миру, чтобы определить, точен ли ответ. Вольфрам отмечает, что 80% времени на уроках математики в школе тратится на третий этап (вычисления вручную). При этом способность работников делать вычисления не нужна работодателям: это могут делать калькуляторы или компьютеры. Вольфрам предлагает, чтобы вместо третьего этапа школьники уделяли больше времени этапам 1, 2 и 4.

Вольфрам утверждает, что в наше время работодателям необходимы люди, которые умеют задавать верные вопросы, разрабатывать модели, анализировать результаты и интерпретировать ответы, а не быстро выполнять вычисления, как раньше.

В список Fortune 500 входят 500 крупнейших компаний США. Когда в 1970 году руководителей этих компаний спросили, какие качества новых сотрудников представляют для них самую большую ценность, ответы выглядели так (табл. 3.1).

Таблица 3.1.Самые ценные качества сотрудников компаний из списка Fortune 500, по состоянию на 1970 год

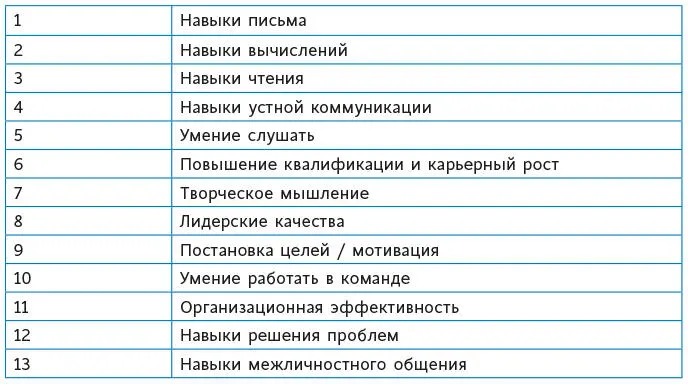
Навыки вычислений занимали второе место в списке. В 1999 году список выглядел так, как показано в таблице 3.2.

Таблица 3.2.Самые ценные качества сотрудников компаний из списка Fortune 500, по состоянию на 1999 год

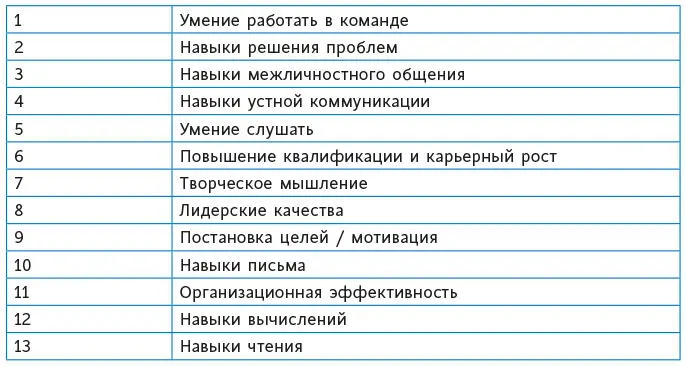
Навыки вычислений опустились на предпоследнее место в списке, а первые места заняли умение работать в команде и навыки решения задач.

Часто родители не видят нужды в строгости, которая составляет суть математики. Многие спрашивали меня: зачем ребенку объяснять свою работу, если он может получить верное решение? Мой ответ неизменен: объяснение называется в математике рассуждением, а рассуждение — обязательное условие математической строгости. Специалисты по естественным наукам доказывают или опровергают теории путем поиска реальных ситуаций, в которых эти теории работают или не работают. Математики доказывают теории в рамках обоснования. Им необходимо привести аргументы, которые убедят других, тщательно выстраивая цепочку рассуждений от одной идеи к другой с помощью логических связей. Математика — сугубо социальная наука, поскольку доказательство возникает только тогда, когда математики могут убедить коллег в наличии логических связей.

Многие работы по математике — плод совместного труда. Леоне Бертон изучала работу математиков и пришла к выводу, что более половины их публикаций подготовлены в соавторстве (Burton, 1999). Но на многих уроках математики ученики в полной тишине заполняют листы с заданиями. В то время как очень важно обсуждать задачи в группах или всем классом. Это самый эффективный инструмент осмысления материала (ученики редко усваивают идеи, не обсудив их); оно делает предмет интереснее и вовлекает детей в процесс обучения. Кроме того, во время обсуждения школьники учатся рассуждать логически и критиковать мнения друг друга, а оба этих качества очень востребованы в современных компаниях. В мире высоких технологий почти все новые профессии подразумевают работу с большими объемами данных, постановку вопросов и поиск способов достижения целей на основе логических рассуждений. Конрад Вольфрам сказал мне, что любой, кто не способен делать математические умозаключения, не сможет эффективно выполнять свои обязанности на рабочем месте. Когда сотрудники рассуждают и обсуждают математические способы решения проблем, их коллеги могут сформулировать новые идеи на основе этих способов, а также определить, нет ли здесь ошибки. Командная работа, которую так высоко ценят работодатели, основана на математическом рассуждении. Люди, которые просто выдают результаты вычислений, не приносят пользы; они должны уметь обосновывать полученные результаты.

Кроме того, необходимо, чтобы ученики рассуждали на уроках математики, поскольку сам акт осмысления задачи и анализа рассуждений другого человека вызывает интерес . Ученики и взрослые гораздо активнее участвуют в работе, когда им дают открытые задачи и разрешают предлагать свои методы и пути решения, чем в работе над задачами, требующими вычислений и ответа. В главе 5представлено много содержательных математических задач, требующих логических рассуждений, а также показаны некоторые способы их составления.

В сфере обучения математике часто возникает и другая проблема: люди убеждены в том, что эта дисциплина сводится к вычислениям, а лучшие математические умы — люди, которые умеют быстро вычислять. Более того, некоторые считают, что успешно заниматься математикой может только тот, кто умеет быстро думать. Но многие математики, которых можно считать весьма одаренными людьми, выполняют вычисления медленно , потому что их рассуждения очень тщательны и глубоки.

Лоран Шварц получил Филдсовскую премию и был одним из величайших математиков своего времени. Однако в школе он решал математические задачи медленнее всех одноклассников. В автобиографии «Математик, преодолевающий трудности своего столетия», опубликованной в 2001 году, Шварц вспоминает свои школьные годы и говорит, что он чувствовал себя глупым, поскольку в его школе ценилась способность быстро думать, а он размышлял медленно и глубоко.