Джо Боулер - Математическое мышление

Математическое мышление подразумевает активный подход к познанию, при котором ученики видят свою задачу в понимании и осмыслении материала. Чувство числа отражает глубокое понимание математики, и оно формируется при применении математического мышления, суть которого — в наполнении чисел и количества смыслом. Нужно развивать чувство числа у учеников — не только потому, что это основа высшей математики (Feikes & Schwingendorf, 2008), но и потому, что оно помогает сформировать математическое мышление, и знание способов развития одного способствует развитию другого.

На рисунке 4.1 стрелками обозначены методы, которые необходимо изучить, а в ячейках отражены изучаемые концепции. В нижнем левом углу представлен метод счета. Когда ученики учатся считать, они запоминают порядок и названия чисел, но у них формируется и концепция числа — представление о нем. В самом начале обучения сложению ученики осваивают метод «продолжение счета». Он используется, когда заданы два числа (например, 15 и 4). В этом случае вы осваиваете сложение так: сначала считаете до 15, а затем продолжаете счет — 16–17–18–19. Изучая метод продолжения, ученики усваивают понятие суммы. Речь не о методе сложения, а о самой идее. На следующем этапе можно научиться складывать группы чисел, например три числа 4. Когда ученики осваивают этот навык, у них формируется концепция произведения. Здесь снова речь не о методе (в данном случае умножения), а об идее. Концепции числа, суммы и произведения требуют глубоких размышлений. Изучение методов, например сложения и умножения, должно быть не самоцелью, а элементом концептуального понимания чисел, суммы и произведения, а также их соотношения

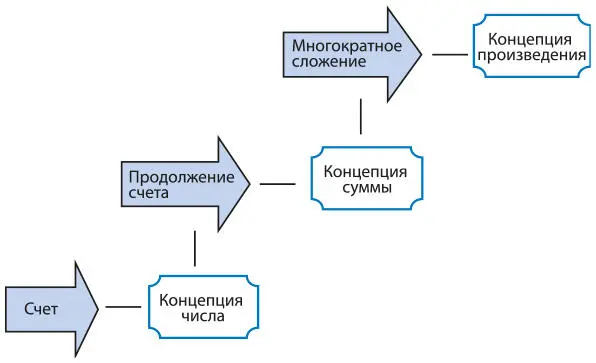
Рис. 4.1.Математические методы и концепции

Источник: Gray & Tall, 1994.

Когда мы занимаемся математикой, в нашем мозге происходит процесс сжатия . Когда вы изучаете область, о которой ничего не знаете, она занимает много места в вашем мозге: ведь вам нужно напряженно размышлять, как это работает и как разные концепции соотносятся друг с другом. Но математические понятия, которые вы изучили ранее и хорошо знаете (например, сложение), занимают в мозге небольшое пространство. Вы можете использовать эти знания, даже не задумываясь. Процесс сжатия происходит потому, что головной мозг — крайне сложный орган, контролирующий много разных процессов, и в любой момент он может сосредоточиться только на нескольких несжатых концепциях. Те же, которые вы хорошо знаете, сжимаются и архивируются. Уильям Терстон, выдающийся математик, получивший Филдсовскую премию, так описывает процесс сжатия.

Математика поразительно легко поддается сжатию: вы можете долго и напряженно трудиться, шаг за шагом прорабатывая один процесс или идею с нескольких точек зрения. Но как только вы по-настоящему поймете нечто и сможете увидеть это как единое целое, скорее всего, произойдет очень сильное ментальное сжатие. Вы можете отправить эту информацию в архив, а при необходимости быстро и полностью восстановить и использовать ее всего лишь за один шаг в рамках другого ментального процесса. Озарение, которым сопровождается такое сжатие, — одна из истинных радостей математики (Thurston, 1990).

Многие ученики не считают, что математика дарит «истинную радость» — отчасти потому, что в их мозге сжатия не происходит. Мозг способен сжимать только концепции, но не правила и методы. Следовательно, у учеников, которые не мыслят концептуально, а воспринимают математику как список правил, подлежащих запоминанию, сжатия не происходит, и их мозг не может упорядочивать концепции и архивировать их, а пытается хранить длинные списки методов и правил. Именно поэтому важно воспитать концептуальный подход к математике — основу математического мышления.

Многие убеждены, что невозможно постоянно размышлять над математикой на концептуальном уровне, поскольку существует много фактов (например, 8 × 4 = 32), которые надо запомнить. Однако все факты можно осваивать и запоминать в рамках концептуального подхода. К сожалению, большинство учителей и родителей считают, что некоторые области математики основаны на фактах (например, о числах) и их необходимо бездумно оттачивать и быстро заучивать. Но такой подход в первые годы в школе вредит ученикам, заставляя их думать, что преуспевать в математике — значит быстро вспоминать факты, и мешает им развивать математическое мышление.

Сами математические факты — лишь небольшая часть науки, и их лучше изучать путем применения чисел разными способами и в разных ситуациях. К сожалению, часто математические факты рассматриваются по отдельности и у учеников создается впечатление, будто это суть дисциплины и, что еще хуже, умение быстро восстанавливать такие факты в памяти — признак хорошего ученика. Обе эти идеи ошибочны, их нельзя внушать ученикам. Ведь именно они приводят к появлению разочаровавшихся учеников, боящихся математики.

Я росла в Англии в прогрессивную эпоху, когда начальные школы были ориентированы на развитие цельной личности, поэтому мне не приходилось учить наизусть таблицы сложения, вычитания и умножения. Я никогда не заучивала факты, но могу быстро сгенерировать любой из них, поскольку у меня есть чувство числа и я освоила эффективные способы анализа числовых комбинаций. Отказ от заучивания никогда не был сдерживающим фактором для меня. И я стала профессором математики, поскольку у меня есть чувство числа, овладеть которым для учеников гораздо важнее, чем запомнить факты. Процесс формирования этого чувства сводится к изучению математических фактов вместе с глубоким пониманием чисел и их соотношений.

Примерно у трети учеников страх перед математикой возникает после того, как они начинают сдавать тесты с ограничением времени (Boaler, 2014c). Сайен Бейлок и ее коллеги изучали мозг участников исследования с помощью МРТ и пришли к выводу, что математические факты хранятся в кратковременной памяти. Но когда ученики находятся в состоянии стресса (например, если им приходится отвечать на вопросы в условиях ограничения времени), кратковременная память блокируется и ученики не могут получить доступ к математическим фактам, которые они знают (Beilock, 2011). Когда ученики осознают, что не могут эффективно выполнять тесты с ограничением времени, они начинают тревожиться и теряют уверенность в своих математических способностях. Блокировка кратковременной памяти и связанная с этим тревога особенно распространены среди сильных учеников и девочек. По самым скромным оценкам, минимум треть учеников испытывает очень сильный стресс во время тестов с ограничением времени, причем независимо от своей успеваемости или уровня благосостояния. Если мы постоянно подвергаем учеников такому испытанию, можно считать их потерянными для математики.