Джо Боулер - Математическое мышление

Ученикам в возрасте 11 лет показали следующий рисунок и задали вопрос: прямая a параллельна прямой c ?

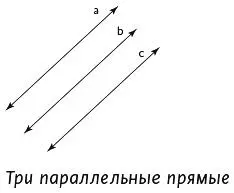
Большинство учеников дали ответ: «Нет, потому что между ними находится прямая b ». Причина в том, что понятие параллельности почти всегда иллюстрируют рисунком с двумя прямыми.

Затем учеников попросили назвать следующую фигуру.

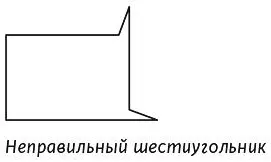
Большинство не смогли этого сделать. На рисунке изображен шестиугольник (многоугольник с шестью сторонами), но шестиугольники почти всегда показывают в таком виде.

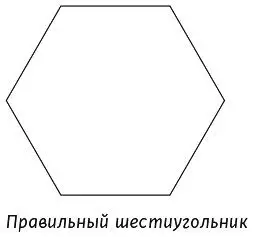
Это не отражает в полной мере концепцию шестиугольника.

Более половины учеников восьми лет не воспринимают представленные ниже фигуры как прямой угол, треугольник, квадрат и параллельные прямые…

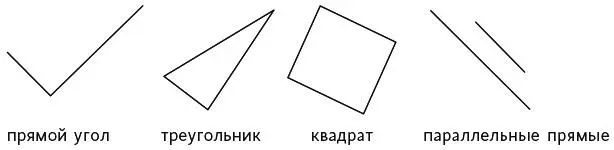
Незнакомые изображения геометрических концепций

…поскольку им всегда показывают самый простой вариант. Вот знакомые изображения, которые ученики ожидают увидеть.

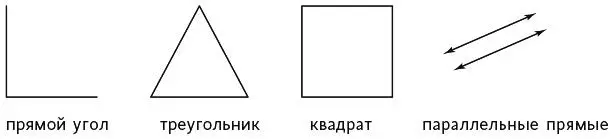
Знакомые изображения геометрических концепций

Итак, более половины учеников, принимавших участие в исследовании, не смогли правильно назвать фигуры. И вот что это значит: когда в учебниках приводится только самый простой вариант идеи, ученики не могут узнать, в чем состоит ее суть. Дети не смогли правильно опознать разные объекты, поскольку авторы учебников неизменно приводят «идеальные примеры». Когда ученики изучают какое-то понятие, вместо идеальных примеров целесообразно предлагать им разные, чтобы некоторые из них едва отвечали этому определению, а некоторые вообще не соответствовали ему.

Учителя математики должны также давать достаточно широкое определение той концепции, которую изучают ученики, и иногда это лучше всего сделать с помощью правдоподобных, но ложных примеров . В процессе изучения определения часто полезно приводить как примеры, отвечающие ему, так и не отвечающие ему, а не идеальные варианты. Например, когда ученики изучают птиц, стоит напомнить им о летучих мышах и предложить подумать, почему они не относятся к птицам, а не рассматривать все больше изображений воробьев, ворон и других птиц.

Неправильное понимание концепций, возникающее у учеников при рассмотрении идеальных примеров, аналогично проблемам, возникающим при отработке обособленных методов. Ученикам дают несложные ситуации, требующие простого применения процедур (а во многих случаях никаких ситуаций и нет). Ученики изучают метод, но, когда им дают математические задачи или нужно использовать математику в реальном мире, они не могут применить его (Organisation for Economic Co-operation and Development, 2013). Реальные задачи зачастую требуют отбора и адаптации методов, применению которых дети никогда не учились и даже не знают о них. В следующей главе мы проанализируем характер содержательных математических задач, позволяющих избежать таких проблем.

В ходе знаменитого научного исследования в Англии я три года отслеживала успеваемость учеников при применении подхода к изучению математики, основанного на практике. Дети снова и снова отрабатывали на уроках обособленные примеры (Boaler, 2002a). Я сравнила их результаты с результатами, полученными в случае, когда ученикам демонстрировали всю сложность математики. При этом предполагалось, что дети должны постоянно размышлять на концептуальном уровне, выбирая и применяя те или иные методы. Два этих подхода к преподаванию математики использовались в разных школах в работе с учениками одинакового происхождения и уровня успеваемости, причем обе школы находились в небогатых районах. Дети, которых учили многократно отрабатывать методы в школе с жесткими требованиями ко времени выполнения заданий, получили гораздо более низкие оценки во время государственного экзамена по математике по сравнению с теми, кого стимулировали размышлять на концептуальном уровне. Во время государственного экзамена (включающего ряд процедурных вопросов) ученики традиционной школы столкнулись с серьезной проблемой: они не знали, какой метод выбрать, чтобы найти ответы. Они многократно отрабатывали методы, но им никогда не предлагали проанализировать ситуацию и выбрать подходящий. Вот размышления двух учеников этой школы о трудностях, с которыми они столкнулись во время экзамена.

Это глупо. Когда ты на уроке выполняешь задание (даже трудное), то получаешь от силы один-два неправильных ответа. Но большинство ответов правильные, и ты думаешь: «Ну вот, когда будет экзамен, я смогу ответить на большинство вопросов правильно». Ведь ты правильно понял все темы. А на самом деле ты ничего не понял (Алан, Эмбер-Хилл).

Все совсем иначе. Все не так, как тебе говорили, — описание, вопрос; все не так, как в учебниках, как объясняет учитель (Гэри, Эмбер-Хилл).

Чересчур упрощенный подход к математике — одна из причин проблем в ее изучении. Вдобавок у учеников не развивается математическое мышление: им внушают, что на уроках математики нет места размышлениям и осмыслению концепций, требуется лишь многократное повторение определенных методов.

В ходе еще одного исследования, которое было проведено в США, мы спрашивали детей, которых обучали математике по модели отработки методов, какова их роль на уроках по этому предмету (Boaler & Staples, 2005). Поразительно много учеников (97%) дали один и тот же ответ: «Максимально сосредоточиться». Этот пассивный акт наблюдения (а не размышлений, построения логических выводов или осмысления) не приводит к пониманию предмета или формированию математического мышления.

Ученикам часто дают практические задания по математике на дом. Но многие данные демонстрируют, что домашние задания в любой форме бесполезны или губительны (подробнее см. главу 6). У меня есть дети, и домашние задания — самая распространенная причина слез в нашем доме, а математика — предмет, работа над которым дома вызывает у детей самый сильный стресс, особенно если задание представляет собой длинный список разрозненных вопросов.