Джо Боулер - Математическое мышление

Я беседую о стандартах Common Core по математике со многими родителями, и мне часто задают такой вопрос (особенно родители сильных учеников): «Зачем моему ребенку обсуждать свою работу в группе, если он может сам получить все ответы?» Я говорю таким родителям, что объяснение своей работы — практика, которая называется логическим рассуждением и лежит в основе математики. Когда ученики выдвигают доводы в пользу своих идей и обосновывают свой ход мыслей, они занимаются истинной математикой. Ученые предлагают теории и ищут примеры, которые доказывают или опровергают эту теорию. Математики предлагают теории и рассуждают о своих математических методах, обосновывая установленные ими логические связи между этими идеями (Boaler, 2013c).

В главе 5шла речь об учебной стратегии, в соответствии с которой ученикам предлагают быть скептиками, побуждая друг друга к высокому уровню рассуждений. Это превосходный способ научить учеников рассуждать и брать на себя роль скептиков, что им очень нравится. Как было сказано в главе 5, рассуждение — не только важнейшая математическая практика, но и учебная, которая обеспечивает равенство, предоставляя всем доступ к идеям. Выступая в роли скептиков, ученики получают возможность задавать вопросы другим; при этом им не приходится брать на себя роль того, кто ничего не понимает.

Используйте современные технологии и развивающие материалы

Показывая ученикам мир открытой, визуальной и творческой математики, целесообразно использовать разные элементы современных технологий и развивающие материалы. Счетные палочки Кюизенера, соединяющиеся кубики и занимательная мозаика помогают учащимся на всех уровнях; я использую их даже в работе со студентами Стэнфорда. В главе 4представлен анализ приложений и игр, которые также развивают концептуальное и визуальное мышление. В главе 4 я сфокусировалась на числах, но есть много хороших приложений, позволяющих ученикам исследовать геометрические идеи в двух или трех измерениях, перемещая углы и прямые, чтобы изучить соотношения. Это важные и эффективные размышления, которые невозможно выполнить с помощью ручки и бумаги. Приложения Geometry Pad для iPad и GeoGebra позволяют учителям и ученикам создавать свои динамичные изображения и исследовать геометрические и алгебраические понятия, такие как y = mb + x , и тригонометрические функции в режиме динамического визуального отображения. Приложение Geometry Pad выпускает компания Bytes Arithmetic; его базовая версия есть в бесплатном доступе.

Другие приложения, например Tap Tap Blocks, помогают ученикам строить объекты в трех измерениях, создавая и решая пространственные и алгебраические закономерности (см. рис. 9.12). Ученики могут размещать и вращать объекты в искусственно созданном трехмерном пространстве. Tap Tap Blocks — бесплатное приложение, работающее на базе iOS, которое разработал Пол Хангас.

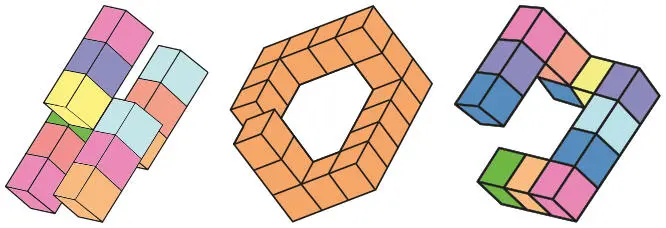
Рис. 9.12.Tap Tap Blocks

С помощью приложения можно предложить ученикам выполнить такое задание: создать фигуру, сделать несколько ее скриншотов с разных сторон, а затем предложить одному из друзей составить свою фигуру (см. рис. 9.13).

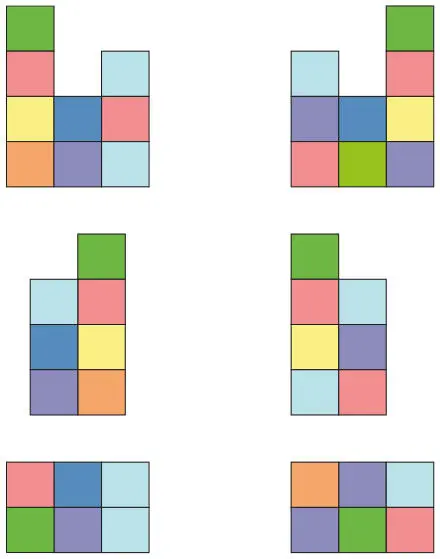
Рис. 9.13.Вид фигуры, созданной в приложении Tap Tap Blocks, с шести разных сторон

Можешь ли ты построить свою фигуру, в которой 1 оранжевый, 1 желтый, 1 синий, 2 зеленых, 2 голубых, 2 красных и 3 фиолетовых блока? Вот несколько скриншотов этой фигуры с разных сторон.

Все эти программы предлагают эффективный способ вовлечения учеников в процесс концептуального и визуального мышления, но есть и другие приложения, игры и сайты, обеспечивающие такую возможность. Существует множество приложений и игр, которые якобы могут помочь ученикам, но немногие из них опираются на результаты исследований по теме обучения, чтобы представить математику как концептуальную и визуальную дисциплину. Я рекомендую избирательно подходить к выбору технологий для работы с учениками и использовать только то, что стимулирует их размышлять и выдвигать гипотезы, а не развивать скорость выполнения процедур и вычислений.

Математика — широкая, многоплановая дисциплина, и когда учителя будут учитывать ее многоплановость при преподавании и оценке знаний, гораздо больше учеников получат доступ к математике и испытают воодушевление в связи с этим. Открывая математику, мы увеличиваем число и расширяем круг учеников, которые смогут успешно заниматься этой дисциплиной. Это не искусственное расширение или упрощение; это скорее такое расширение, которое приближает школьную математику к истинной и к математике реального мира.

У учителей, родителей и руководителей есть возможность направить учеников на математический путь, ориентированный на мышление роста, который приведет их к большим достижениям, счастью и высокой самооценке на протяжении всей жизни. Необходимо избавить молодых людей от деструктивных представлений о том, что неудачи недопустимы, нельзя совершать ошибки, математика доступна только избранным, а успех должен даваться легко. Необходимо приобщить их к творческой, красивой математике, позволяющей ставить вопросы, которых еще никто не ставил, или выдвигать идеи, выходящие за традиционные и мыслимые пределы. Надеюсь, эта книга подарила вам идеи, которые помогут вам начать или возобновить свой путь к творческой, развивающей математике и мышлению роста, по которому вы будете следовать всю жизнь. Создавая условия для открытой математики и подавая сигналы в отношении изучения этой дисциплины, которые ее поддерживают, мы формируем свою интеллектуальную свободу в качестве учителей и родителей, а также пробуждаем такую свободу в других людях.

Благодарю вас, что отправились в это путешествие вместе со мной. Теперь пришло время привлечь других на тот путь, о котором вы здесь узнали, предложив им стать такими, какими они должны быть: свободными от искусственных правил и вдохновленными знанием о том, что у них есть безграничный математический потенциал. Все мы можем открыть математику и дать ученикам шанс ставить вопросы и проявить естественную изобретательность и любознательность при изучении этой дисциплины. Обеспечив детям такой опыт изучения творческой, развивающей математики, мы изменим их и их способы взаимодействия с окружающим миром.

Предоставив ученикам свободу, мы получим красивую математику.

Гладуэлл М. Гении и аутсайдеры.М.: Манн, Иванов и Фербер, 2016.