Яков Перельман - Занимательная арифметика [Загадки и диковинки в мире чисел]

Старинная квитанция в уплате ясака (подати) на сумму 1232 руб. 24 коп., написанная народными цифровыми знаками.

Как видите, употребляемые нами арабские и римские цифры — не единственный способ обозначения чисел. В старину применялись у нас другие системы письменного счисления, отдаленно сходные с римскими и совсем не сходные с арабскими цифрами.

Но и это еще не все способы изображения чисел, какие были в употреблении: многие торговцы, например, имели свои секретные знаки для числовых обозначений — так называемые торговые "меты". О них побеседуем сейчас подробнее.

В дореволюционное время на вещах, купленных у офеней [4] Офеня — бродячий торговец, разносчик, продававший по деревням галантерею, мануфактуру, книжки, лубочные картинки. или в частных магазинах, особенно провинциальных, можно было зачастую заметить непонятные буквенные обозначения вроде

а ве в уо.

Это не что иное, как цена веши без запроса, которую торговец обозначал на товаре, но так, однако, чтобы ее не мог разгадать покупатель. Бросив взгляд на эти буквы, торговец сразу проникал в их скрытый смысл и, сделав надбавку, называл покупателю цену с запросом.

Система обозначения была весьма проста. Торговец выбирал какое-нибудь слово, составленное из 10 различных букв; чаще всего останавливали выбор на словах: трудолюбие, правосудие, миролюбецъ, Миралюбовъ . Первая буква слова обозначала 1, вторая — 2, третья — 3 и т. д.; десятою буквою обозначался ноль. С помощью этих условных букв-цифр торговец и обозначал на товарах их цену, храня в строгом секрете "ключ" к своей системе прибылей.

Если, например, выбрано было слово:

п р а в о с у д и е

1 2 3 4 5 6 7 8 9 0

то цена 4 руб. 75 коп. обозначалась так:

в уо.

Иногда цена на товаре писалась в виде дроби; например, на одной из купленных мною книг (см. рисунок) имеется обозначение

ое/mро

Это значит, при ключе "трудолюбие", что надо запросить 1 руб. 25 коп., себе же книга стоила 50 коп.

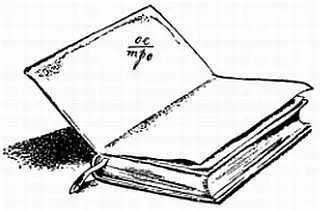
Цена книги, записанная торговцем при помощи секретного десятибуквенного слова. Запись означает, что книга стоит себе 50 коп., а продается за 1 руб. 25 коп.

После только что сказанного легко сообразить, что числа можно изображать не только с помощью цифр но и с помощью любых иных знаков или даже предметов: карандашей, перьев, линеек, резинок и т. п., надо только условиться приписывать каждому предмету значение какой-нибудь определенной цифры. Можно даже, ради курьеза, с помощью таких цифр-предметов изображать действия над числами: складывать, вычитать, умножать, делить.

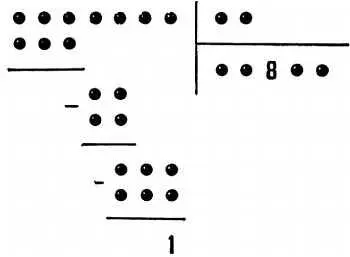
Попробуйте доискаться значения всех цифр этого деления!

В одном зарубежном шахматном журнале была предложена задача: раскрыть истинный смысл следующего примера деления чисел, в котором почти все цифры заменены пешками (на нашем рисунке — черными кружками). Из 28 цифр известны только две: одна (8) в частном и другая (1) в остатке. Казалось бы, доискаться значения прочих 26 цифр, обозначенных кружками, немыслимо. Между тем это сравнительно несложная задача для каждого, кто отчетливо представляет себе смысл отдельных операций, входящих в состав действия деления.

Вот какой ход рассуждений приводит нас к цели.

Вторая цифра частного есть, конечно, 0. Это следует из того, что к остатку от первого вычитания снесена не одна цифра, а две: ясно, что после снесения первой цифры составилось число, меньшее делителя; а в таких случаях очередная цифра частного 0.

По сходным основаниям заключаем, что четвертая цифра частного также 0.

Всматриваясь в расположение кружочков, замечаем, что двузначный делитель, будучи умножен на 8, дает число двузначное; когда же его умножают на первую (пока неизвестную) цифру частного, получается число из трех цифр. Значит, эта первая цифра частного больше 8; такой цифрой может быть только 9.

Сходным образом устанавливаем, что и последняя цифра частного — 9.

Теперь частное определилось: 90 809. Остается раскрыть смысл делителя. Делитель состоит, мы знаем, из двух цифр; кроме того, расположение кружков говорит о том, что это двузначное число при умножении на 8 дает также двузначное число; при умножении же на 9 оно дает произведение, состоящее уже из трех цифр. Что же это за число? Производим испытания, начиная с наименьшего двузначного числа — 10:

10 х 8 = 80,

10 х 9 = 90.

Число 10, как видим, не удовлетворяет требуемым условиям: оба произведения двузначные. Испытываем следующее двузначное число — 11:

11 х 8 = 88,

11 х 9 = 99.

Число 11 также, очевидно, не годится: оба произведения снова двузначные. Испытываем 12:

12 х 8 = 96,

12 х 9 = 108.

Число 12 удовлетворяет всем требованиям. Нет ли еще таких чисел? Испытаем 13:

13 х 8 = 104,

13 х 9 = 117.

Оба произведения трехзначные; следовательно, 13 не годится. Ясно, что неподходящими являются и все числа, большие чем 13.

Итак, единственный возможный делитель — 12. Зная делитель, частное и остаток, легко находим делимое и восстанавливаем весь случай деления.

Итак,

делимое = 90 809 х 12 + 1 = 1 089 709.

Случай деления:

Как видим, по двум известным цифрам нам удалось установить смысл 26 неизвестных цифр.

Перед нами ряд действий над числами, обозначенными предметами сервировки стола (см. рисунок). Вилка, ложка, нож, кувшинчик, тарелка — все это знаки, каждый из которых заменяет определенную цифру.

Глядя на эту группу ножей, вилок, посуды и т. п., попробуйте угадать: какие именно числа здесь обозначены?

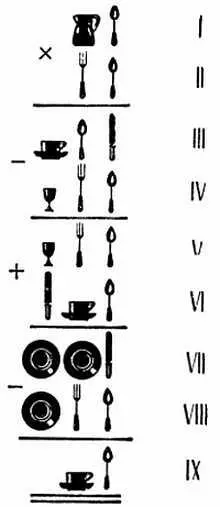
Разгадайте, над какими числами производятся обозначенные здесь арифметические действия!

С первого взгляда задача кажется очень трудной: приходится разгадывать настоящие иероглифы [5] Иероглиф — фигурный знак, обозначающий или целые понятия, или отдельные слоги и звуки речи. , как сделал некогда француз Шампольон [6] Шампольон (1790–1832) — знаменитый французский филолог, основатель египтологии — науки, изучающей язык, историю и культуру древнего Египта и прилегающих к нему стран. . Но ваша задача гораздо легче. Вы ведь знаете, что числа здесь, хотя обозначены вилками, ножами, ложками и т. п., написаны по десятичной системе счисления, то есть вам известно, что тарелка, стоящая на втором месте (считая справа), есть цифра десятков, что предмет направо от нее — цифра единиц, а по левую сторону — цифра сотен. Кроме того, вы знаете, что расположение всех этих предметов имеет определенный смысл, который вытекает из сущности арифметических действий, производимых над обозначенными ими числами. Все это может значительно облегчить вам решение предложенной задачи.