Яков Перельман - Занимательная арифметика [Загадки и диковинки в мире чисел]

Вот как можно доискаться значения расставленных здесь предметов. Рассматривая первые три ряда на нашем рисунке, вы видите, что "ложка", умноженная на "ложку", дает "нож". А из следующих рядов видно, что "нож" без "ложки" дает "ложку " или что "ложка прибавленная к "ложке", дает "нож". Какая же цифра дает одно и то же и при удвоении и при умножении сама на себя? Это может быть только 2, потому что 2 х 2 = 2 + 2. Таким образом узнаём, что "ложка" обозначает 2 и, следовательно, "нож" — 4.

Теперь идем дальше. Какая цифра обозначена "вилкой"? Попробуем разгадать это, присмотревшись к первым трем рядам, где "вилка" участвует в умножении, и к рядам III, IV и V , где та же "вилка" фигурирует в действии вычитания. Из группы вычитания вы видите, что, отнимая в разряде десятков "вилку" от "ложки", получаем в результате "вилку", то-есть при вычитании "вилки" из двойки получается "вилка". Это может быть в двух случаях: либо "вилка" обозначает 1, и тогда 2 – 1 = 1; либо же "вилка" обозначает 6, и тогда, вычитая 6 из 12 (единица высшего разряда занимается у "чашки"), получаем 6.

Что же выбрать: 1 или 6? Испытаем, годится ли 6 для "вилки" в других действиях. Обратите внимание на сложение V и VI рядов: "вилка" (то-есть 6), прибавленная к "чашке", дает "тарелку"; значит, "чашка" должна быть меньше 4 (потому что в рядах VII и VIII при вычитании "вилки" из "тарелки" получается "чашка"). Но "чашка" не может обозначаться двойкой, так как двойка обозначена уже "ложкой"; не может "чашка" быть и единицей — иначе вычитание IV ряда из III не могло бы дать трехзначного числа в V ряду. Не может, наконец, "чашка" обозначать и 3 — вот почему :если "чашку" принять за 3, то "бокальчик" (ряды IV и V ) должен быть принят за единицу, потому что 1 + 1 = 2, то-есть "бокальчик", прибавленный к "бокальчику", дает "чашку", убавленную на единицу, которая была занята у него при вычитании в разряде десятков; "бокальчик" же не может быть принят за единицу, потому что тогда "тарелка" в VII ряду будет обозначать в одном случае цифру 5 ("бокальчик", сложенный с "ножом"), а в другом — цифру 9 ("вилка", прибавленная к "чашке"), чего быть не может. Значит, нельзя было "вилку" принимать за 6, а надо было принять ее за единицу.

Узнав путем таких — довольно, правда, долгих — поисков, что "вилка" обозначает цифру 1, мы дальше идем более уверенно и быстро. Из действия вычитания в III и IV рядах видим, что "чашка" обозначает либо 6, либо 8. Но 8 приходится отвергнуть, потому что тогда вышло бы, что "бокальчик" должен обозначать 4, а мы знаем, что цифра 4 обозначена "ножом". Итак, "чашка" обозначает цифру 6, а следовательно, "бокальчик" — цифру 3.

Какая же цифра обозначена "кувшинчиком" в I ряду? Это легко узнать, раз нам известно произведение ( III ряд, 624) и один из множителей ( II ряд, 12). Разделив 624 на 12, получаем 52. Следовательно, "кувшинчик" обозначает 5.

Значение "тарелки" определяется просто: в VZ/ряду «вилка", прибавленная к "чашке", и "бокальчик", прибавленный к "ножу", дают порознь "тарелку", то-есть "тарелка" обозначает число, равное 1 + 6 = 3 + 4 = 7.

Итак, мы путем нехитрых арифметических вычислений разгадали иероглифическую надпись из предметов столовой сервировки:

"кувшин " обозначает 5, "чашка " — 6,

"ложка " — 2, "бокальчик" — 3,

"вилка" — 1, "тарелка" — 7.

"нож" — 4,

А весь ряд арифметических действий, изображенный этой оригинальной сервировкой, приобретает такой смысл:

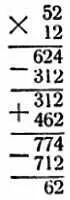
То, что я называю арифметическими ребусами, — занимательная игра школьников: отгадывание задуманного слова решением задачи вроде той, какую мы решили в предыдущей статье. Загадывающий задумывает слово, состоящее из 10 неповторяющихся букв, — например, "трудолюбие", "специально", просвещать". Приняв буквы задуманного слова за цифры, загадывающий изображает посредством этих букв какой-нибудь случай деления. Если задумано слово "просвещать", то можно взять такой пример деления:

Можно взять и другие слова:

Буквенное изображение определенного случая деления вручается отгадчику, который и должен по этому, на первый взгляд бессмысленному, набору букв угадать задуманное слово. Как следует в подобных случаях доискиваться числового значения букв, читатель уже знает: мы объяснили это, когда решали задачу предыдущей статьи. При некотором терпении можно успешно разгадывать эти арифметические ребусы, если только пример достаточно длинен и дает необходимый материал для догадок и испытаний. Если же выбраны слова, дающие чересчур короткий случай деления, например:

то разгадывать очень трудно. В подобных случаях надо просить загадывающего продолжить деление до сотых или тысячных долей, то-есть получить в частном еще два или три десятичных знака. Вот пример деления до сотых долей:

Если бы в этом случае мы остановились на целом частном ( со ), отгадка задуманного слова едва ли была бы возможна.

Что касается слов, пригодных в качестве "ключа* для подобных ребусов, то выбор их не так беден, как может казаться; кроме прежде указанных, можно использовать слова:

республика, пятидневка,

демократия, струбцинка.

Как далеко может идти изобретательность в этом направлении, показывает следующий пример. Один из читателей прислал мне остроумно составленный арифметический ребус, разгадка которого представляет собой… лозунг для пропаганды идеи межпланетных путешествий. Ребус состоит из трех частей, последовательно развертывающих этот близкий мне лозунг. Вот они:

Читатель, который пожелает разгадать этот тройной (и весьма нелегкий) ребус, узнает в итоге, что

Предлагаю далее читателю самостоятельно разгадать следующий ряд ребусов:

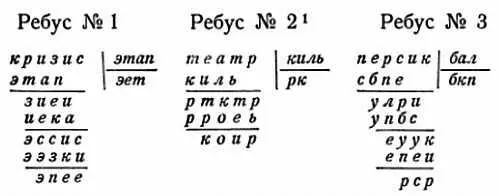
1Хотя в этой задаче ключ состоит из 12 букв и включает в себя повторяющиеся буквы, тем не менее задача вполне разрешима.

Решения этих ребусов см. в ответах.

Особенность десятичной системы счисления остроумно используется даже в такой области, где с первого взгляда этого и ожидать не приходится, — именно, при хранении книг в библиотеке.

Существует такая система распределения книг по номерам, при которой одна и та же книга должна иметь одинаковый номер в любой библиотеке. Это так называемая "десятичная система классификации книг".

Система эта чрезвычайно удобна и весьма несложна. Сущность ее в том, что каждая отрасль знания обозначается определенным числом и притом так, что цифровой состав этого номера сам говорит о месте данного предмета в общей системе знаний.