Виктор Викторов - Пионерский музыкальный клуб. Выпуск 10

— Треугольное число... Может, есть еще какие-нибудь — круглые или пирамидальные?

Вместо ответа мальчик разложил орехи треугольником: в первом ряду — один орех, во втором — два, в третьем — три, и, наконец, в четвертом — четыре.

Треугольник как треугольник. Но при чем здесь все-таки гармония?

Так я этого и не выяснил, потому что капитан, опасаясь, очевидно, как бы я не съел этот ореховый треугольник, увел меня к следующему столу, где другой юный древний грек делил целые числа. И что бы вы думали? Оказалось, что и он тоже занимается гармонией: ищет гармонию числовых отношений. Чудн о !

— Ничего чудн о го, — возразил грек. — В числах тоже есть своя гармония. И основана она на отношениях все тех же четырех чисел: 1, 2, 3 и 4.

Он поманил меня пальцем и благоговейным шепотом сообщил, что эти замечательные гармонические отношения обнаружил великий Пифагор.

Пифагор, Пифагор... У меня от этого имени уже в ушах стреляет: пиф-паф, пиф-паф! И я очень обрадовался, когда капитан схватил меня за руку и потащил к третьему столу. Длинному-предлинному. За ним работал уже не мальчик, а самый что ни на есть настоящий древний грек — старик с курчавой бородой.

— Гипп а с, ученик великого Пифагора, — представился он.

Опять Пифагор! Я только вздохнул.

Побеседовав со стариком, мы узнали, что он возглавляет сейчас пифагорейскую школу.

На столе у Гипп а са лежала длинная линейка.

— Наконец-то хоть что-то математическое, — подумал я. Но и Гиппас тоже, оказывается, изучал гармонию. На сей раз — гармонию звуков.

Бородач натянул на линейку струну, ущипнул ее, и она издала низкий гудящий звук. Потом он прижал струну пальцем ровно посередине и предложил мне ущипнуть одну из ее половинок. Я не заставил себя упрашивать. Струна издала звук потоньше.

— Выше на целую октаву, — сказал капитан Единица.

— Как вы говорите? — переспросил Гиппас. — На октаву? Да, да, по-вашему это как раз так и называется.

Он разделил правую половинку струны еще раз пополам и снова

предложил мне ущипнуть эту четвертушку. Струна зазвучала еще выше, и опять на целую октаву. Потом мы отделяли одну восьмую, одну шестнадцатую струны... И каждый раз получали звук на октаву выше предыдущего. У меня даже палец заболел от щипания.

— Долго это будет продолжаться? — спросил я.

— Совсем недолго, — успокоил меня Гиппас. — Пифагор разделил струну всего на семь октав. Правда, у него при этом получился остаток, но он так мал, что не стоит обращать на него внимания. Пифагор его попросту отрезал...

— Уважаемый Гиппас, — сказал я решительно, — скажите, наконец, кто вы — музыкант или математик?

— Что за нелепый вопрос, — загремел Гиппас, да так, что струна на линейке вздрогнула и загудела. — Все мы здесь музыканты-математики. Да, да! Ведь музыка и математика тесно связаны. И та и другая построены на соотношении чисел. Я уже добрых полчаса тебе об этом толкую. Октава, например, получается при делении отрезка струны пополам. Стало быть, это отношение 2:1...

— Допустим, — сказал я примирительно, — но что общего между музыкой и соотношением чисел в ореховом треугольнике?

— Это уже серьезный вопрос, — подобрел Гиппас. — Числа, образующие этот треугольник, имеют прямую связь с музыкой. Вот хоть отношение 3:2.

Гиппас разделил струну на три равные части и прижал пальцем на расстоянии одной трети от конца.

— Видишь, — пояснил он, — струна разделена на две части. Одна из них равна двум третям, другая одной трети. Значит, длина всей струны относится к большей ее части, как 3:2. Тронем большую часть струны, она зазвучит выше, чем вся струна...

— Теперь уже не на октаву, а всего лишь на квинту, — вставил капитан.

— Совершенно верно, — поклонился Гиппас, — по-вашему это называется квинтой. Снова отложим на меньшей части струны две ее трети — получим...

— Новую квинту! — подхватил я.

Гиппас просиял:

— Нет, ты определенно делаешь успехи. Еще раз разделим таким же способом меньшую часть струны. И так далее, пока не дойдем до конца. И окажется, что на струне, состоящей из семи октав, укладывается двенадцать квинт.

— Скажите! — восхитился я. — Точно двенадцать!

— Гм, гм!.. — закашлялся Гиппас. — В том-то и беда, что не совсем точно. Двенадцать квинт чуть-чуть длиннее семи октав.

Правда, разность между ними совсем ничтожна. Если хотите, я ее подсчитаю. Это очень просто. Сложим семь октав, семь отрезков струны:

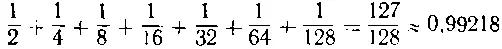
А теперь сложим двенадцать отрезков, образующих квинты:

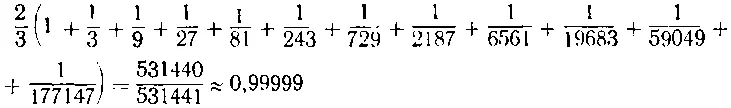
— Остается вычесть из большей суммы меньшую, — сказал я. — 0,99999-0,99218=0,00781. Да, разность и в самом деле очень мала...

— И все же, — возразил Гиппас, — это меня очень расстраивает.

— Очень вам сочувствую, — сказал я. — В ореховом треугольнике есть еще число 4. И вы, помнится, ничего еще не сказали о нем.

— О, отношение 4:3 тоже великолепное! — воодушевился Гиппас. — Оно дает... как это по-вашему?

— Кварту, — подсказал капитан.

— Да, да, кварту, — кивнул Гиппас. —Чтобы получить эту самую кварту, надо заставить звучать три четверти струны. И заметьте, что октава больше квинты как раз на кварту.

— Ну, это еще надо проверить! — усомнился я.

Гиппас насмешливо улыбнулся.

— Чего проще! Раздели отношение 2:1 на 3:2. И получишь...

— Получу четыре третьих, — быстро сосчитал я.

— А это и есть кварта, — подтвердил Гиппас. — Теперь, надеюсь, ты не сомневаешься, что все четыре числа этого орехового или, как назвал его Пифагор, совершенного треугольника находятся между собой в великолепнейшем гармоническом отношении?

— Понятно, — сказал я. — Но что такое октава, квинта и кварта, это мне, по правде говоря, еще все-таки неясно.

Гиппас почесал переносицу:

— Гм... как бы тебе это объяснить? Представь себе, что струна — это лесенка, состоящая из сорока двух ступенек. Представил? Так вот. То, что у вас называется октавой, это всего лишь восемь ступенек этой лестницы. Оттого, собственно, ее и называют октавой. Ведь по-латыни «окто» — восемь. Что же касается кварты, то она состоит из четырех ступенек, квинта — из пяти... Ведь «кварто» и «квинто» по-латински — четыре и пять. А вот разность между квартой и квинтой условились принимать за один музыкальный тон.

— А тон тоже можно выразить числовым отношением? — поинтересовался я. — А то без числовых отношений мне теперь музыка — не музыка.