Виктор Викторов - Пионерский музыкальный клуб. Выпуск 10

Гиппас прямо вспыхнул от удовольствия.

— А как же! Стоит только вычислить, во сколько раз квинта (3:2) больше кварты (4:3).

— Ну, это легче легкого, — отмахнулся я. — 3:2, деленное на 4:3, равно 9:8. И, значит, одному целому тону соответствует отношение девяти к восьми.

— Что за мальчик! — расчувствовался Гиппас. — Между прочим,— добавил он, — числа 8 и 9 тоже за-ме-ча-тель-ны-е! Еще со времен Пифагора мы, его ученики, кроме чисел 1, 2, 3 и 4 очень полюбили другую четверку чисел — 6, 8, 9 и 12.

— Стойте! — закричал я. — Ничего не говорите. Позвольте мне самому разобраться, чем замечательны эти четыре числа. Возьмем сперва отношение 12:6. Оно равно отношению 2:1, то есть октаве. Точно так же отношение 12:8 равно 3:2, а это квинта. И, наконец, отношение 12:9 равно 4:3, то есть кварте. Верно я говорю?

— Верно, дорогой мой друг, — сказал Гиппас, обнимая и целуя меня. — Обидно лишь, что ты не сказал о числе 9. Ведь это же не что иное, как среднее арифметическое между числами 6 и 12.

— А ведь верно! — обрадовался я и тотчас вычислил:

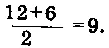
— Гениально! — простонал Гиппас, утирая полой плаща слезы умиления. — Может, скажешь заодно, что такое число 8?

— Наверное, среднее геометрическое между шестью и двенадцатью, — неуверенно предположил я.

— Среднее-то среднее, да только не геометрическое, а гармоническое. И пора бы уж тебе знать, что средним гармоническим двух чисел называется их удвоенное произведение, деленное на их же сумму. Вот, смотри:

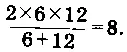
— Уважаемый гармонист, — пробормотал я, — у меня от ваших чисел голова идет кругом...

— Жаль! — огорчился Гиппас. — Ведь я не сказал еще о числе 12. Тоже весьма любопытное число, потому что именно двенадцать квинт уложил Пифагор в семи октавах... Вот, оказывается, какая глубокая связь между числами и музыкой! Впрочем, тебе это ни к чему...

— К чему, очень даже к чему! — горячо заверил я старца. — И огромное вам спасибо за интересную беседу.

Не без сожаления покинули мы с капитаном гостеприимный остров Математа и отправились обратно на фрегат. Всю дорогу сопровождала нас чудесная музыка — плавная, нежная. Только среди приятных звуков иногда вдруг прорывались фальшивые, воющие, будто завыла стая волков. Когда музыка кончилась, голос откуда-то с облаков объявил:

— По просьбе богини Артемиды дельфийский секстет монохордисток исполнил ноктюрн Пифагора.

— Все-таки молодчина этот Пифагор, — расчувствовался я. — Математик и композитор. Ноктюрны сочиняет. Только почему в этом ноктюрне завывают волки?

— Неужели ты не понимаешь, что все дело в разности? — удивился капитан. — В маленькой разности между семью октавами и двенадцатью квинтами? От нее-то и возникает волчий вой при некоторых созвучиях, а лучше сказать — несозвучиях.

— Но почему, — спросил я, — волки завывают только в ноктюрне Пифагора? Ведь в ноктюрнах Шопена никаких волков нет.

Капитан и тут оказался на большой научно-музыкальной высоте. Он объяснил, что Шопен писал музыку совсем для другого, не пифагорейского музыкального строя.

Оказывается, музыканты давным-давно искали способ избавиться от некрасивых созвучий. В этом помогали им многие известные математики — Эйлер, Лейбниц, Лаплас, Паскаль и даже астроном Кеплер. И все-таки никто не смог решить задачу так блестяще, как это сделал в середине XVII века органист Андрей Веркмейстер. Он вышел из положения просто и остроумно: чуть-чуть укоротил квинту. И все двенадцать квинт в точности уложились в семи октавах. А еще Веркмейстер выровнял интервалы между тонами, так что все они расположились равномерно. Капитан сказал, что такое равномерное отношение между тонами называется темперацией. Так вот, она-то и стала основой современного музыкального строя.

Первым темперацию принял великий немецкий музыкант Иоганн Себастьян Бах. И было это в XVIII веке. Бах даже написал замечательное сочинение под названием «Хорошо темперированный клавир».

— С тех пор, — заключил капитан, — почти все крупные композиторы стали пользоваться только этим музыкальным строем.

— Почему почти все? — спросил я.

— Видишь ли, — вздохнул капитан, — новое всегда с трудом пробивает себе дорогу. Великий Бах принял новшество сразу, а его великий современник Гендель так и не признал его.

Когда мы поднялись на фрегат, капитан повел меня в салон и открыл рояль, на котором любил играть в свободное время.

— Вот инструмент современного строя, — сказал он. — Видишь, квинта состоит из трех с половиной тонов (капитан одновременно нажал две клавиши: до и соль). А всего в октаве шесть целых тонов. Если число 6 умножить на 7, то есть на число пифагорейских октав, получится 42. То же число получится, если число квинт в пифагорейской струне (а это 12) умножить на три с половиной. Вот и выходит, что двенадцать квинт точно укладываются в семи октавах. А теперь давай-ка отложим от нижнего до все двенадцать квинт, одну за другой.

Так мы и сделали. И что бы вы думали получилось? Через каждые три с половиной тона мы попадали на другую, ранее не использованную нами ноту: до—соль—ре—ля—ми—си,—фа - диез-до - диез—соль -диез—ре-диез—ля-диез—фа и, наконец, снова до!

— Если все тона этих двенадцати квинт свести в одну октаву, получится двенадцать полутонов хроматической гаммы, — закончил капитан. — В общем, хотя музыкальный строй Пифагора дошел до нас в измененном виде, мы все равно чтим этого великого ученого древнего мира: ведь он первый заставил математику служить музыке и объединил таким образом искусство и науку.

В эту ночь мне снился удивительный сон: Иоганн Себастьян Бах, размахивая дирижерской палочкой, яростно сражался со стаей волков. Волки жалобно выли.

Сегодня, ребята, я даю вам самые разные музыкальные задачи. Вы должны разгадать ребусы, чайнворд, шарады, ответить на вопросы.

Если они покажутся вам очень трудными, не смущайтесь. Чуть-чуть внимания, чуть-чуть настойчивости и вдумчивости — и победа будет одержана. Если же вы все-таки не сумеете ответить на все вопросы, откройте страницу 89. Там есть ответы. Но лучше подумайте еще. Не сегодня, так завтра, послезавтра вы найдете правильное решение.