Миран Липовача - Изучай Haskell во имя добра!

return x

Сопоставление с образцом оканчивается неуспешно, поэтому эффект аналогичен тому, как если бы вся строка с образцом была заменена значением Nothing. Давайте попробуем это:

ghci> wopwop

Nothing

Неуспешно окончившееся сопоставление с образцом вызвало неуспех только в контексте нашей монады, вместо того чтобы вызвать неуспех на уровне всей программы. Очень мило!..

До сих пор вы видели, как значения типа Maybeмогут рассматриваться в качестве значений с контекстом неудачи, и как мы можем ввести в код обработку неуспешно оканчивающихся вычислений, используя оператор >>=для передачи их функциям. В этом разделе мы посмотрим, как использовать монадическую сторону списков, чтобы внести в код недетерминированность в ясном и «читабельном» виде.

В главе 11 мы говорили о том, каким образом списки представляют недетерминированные значения, когда они используются как аппликативные функторы. Значение вроде 5 является детерминированным – оно имеет только один результат, и мы точно знаем, какой он. С другой стороны, значение вроде [3,8,9]содержит несколько результатов, поэтому мы можем рассматривать его как одно значение, которое в то же время, по сути, является множеством значений. Использование списков в качестве аппликативных функторов хорошо демонстрирует эту недетерминированность:

ghci> (*) <$> [1,2,3] <*> [10,100,1000]

[10,100,1000,20,200,2000,30,300,3000]

В окончательный список включаются все возможные комбинации умножения элементов из левого списка на элементы правого. Когда дело касается недетерминированности, у нас есть много вариантов выбора, поэтому мы просто пробуем их все. Это означает, что результатом тоже является недетерминированное значение, но оно содержит намного больше результатов.

Этот контекст недетерминированности очень красиво переводится в монады. Вот как выглядит экземпляр класса Monadдля списков:

instance Monad [] where

return x = [x]

xs >>= f = concat (map f xs)

fail _ = []

Как вы знаете, функция returnделает то же, что и функция pure, и вы уже знакомы с функцией returnдля списков. Она принимает значение и помещает его в минимальный контекст по умолчанию, который по-прежнему возвращает это значение. Другими словами, функция returnсоздаёт список, который содержит только одно это значение в качестве своего результата. Это полезно, когда нам нужно просто обернуть обычное значение в список, чтобы оно могло взаимодействовать с недетерминированными значениями.

Суть операции >>=состоит в получении значения с контекстом (монадического значения) и передаче его функции, которая принимает обычное значение и возвращает значение, обладающее контекстом. Если бы эта функция просто возвращала обычное значение вместо значения с контекстом, то операция >>=не была бы столь полезна: после первого применения контекст был бы утрачен.

Давайте попробуем передать функции недетерминированное значение:

ghci> [3,4,5] >>= \x –> [x,-x]

[3,-3,4,-4,5,-5]

Когда мы использовали операцию >>=со значениями типа Maybe, монадическое значение передавалось в функцию с заботой о возможных неудачах. Здесь она заботится за нас о недетерминированности.

Список [3,4,5]является недетерминированным значением, и мы передаём его в функцию, которая тоже возвращает недетерминированное значение. Результат также является недетерминированным, и он представляет все возможные результаты получения элементов из списка [3,4,5]и передачи их функции \x –> [x,–x]. Эта функция принимает число и производит два результата: один взятый со знаком минус и один неизменный. Поэтому когда мы используем операцию >>=для передачи этого списка функции, каждое число берётся с отрицательным знаком, а также сохраняется неизменным. Образец xв анонимной функции принимает каждое значение из списка, который ей передаётся.

Чтобы увидеть, как это достигается, мы можем просто проследить за выполнением. Сначала у нас есть список [3,4,5]. Потом мы отображаем его с помощью анонимной функции и получаем следующий результат:

[[3,-3],[4,-4],[5,-5]]

Анонимная функция применяется к каждому элементу, и мы получаем список списков. В итоге мы просто сглаживаем список – и вуаля, мы применили недетерминированную функцию к недетерминированному значению!

Недетерминированность также включает поддержку неуспешных вычислений. Пустой список в значительной степени эквивалентен значению Nothing, потому что он означает отсутствие результата. Вот почему неуспешное окончание вычислений определено просто как пустой список. Сообщение об ошибке отбрасывается. Давайте поиграем со списками, которые приводят к неуспеху в вычислениях:

ghci> [] >>= \x –> ["плохой","бешеный","крутой"]

[]

ghci> [1,2,3] >>= \x –> []

[]

В первой строке пустой список передаётся анонимной функции. Поскольку список не содержит элементов, нет элементов для передачи функции, а следовательно, результатом является пустой список. Это аналогично передаче значения Nothingфункции, которая принимает тип Maybe. Во второй строке каждый элемент передаётся функции, но элемент игнорируется, и функция просто возвращает пустой список. Поскольку функция завершается неуспехом для каждого элемента, который в неё попадает, результатом также является неуспех.

Как и в случае со значениями типа Maybe, мы можем сцеплять несколько списков с помощью операции >>=, распространяя недетерминированность:

ghci> [1,2] >>= \n –> ['a','b'] >>= \ch –> return (n,ch)

[(1,'a'),(1,'b'),(2,'a'),(2,'b')]

Числа из списка [1,2]связываются с образцом n; символы из списка ['a','b']связываются с образцом ch. Затем мы выполняем выражение return (n, ch)(или [(n, ch)]), что означает получение пары (n, ch)и помещение её в минимальный контекст по умолчанию. В данном случае это создание наименьшего возможного списка, который по-прежнему представляет пару (n, ch)в качестве результата и обладает наименее возможной недетерминированностью. Его влияние на контекст минимально. Мы говорим: «Для каждого элемента в списке [1,2]обойти каждый элемент из ['a','b']и произвести кортеж, содержащий по одному элементу из каждого списка».

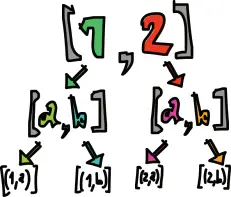
Вообще говоря, поскольку функция returnпринимает значение и оборачивает его в минимальный контекст, она не обладает какими-то дополнительными эффектами (вроде приведения к неуспешному окончанию вычислений в типе Maybeили получению ещё большей недетерминированности для списков), но она действительно возвращает что-то в качестве своего результата.