А. Григорьев - О чём не пишут в книгах по Delphi

var

Pt: TPoint;

begin

// Чтобы правильно обрабатывать стандартную неклиентскую область,

// вызываем унаследованный обработчик

inherited;

// Не забываем, что параметры WM_NCHITTEST дают экранные,

// а не клиентские координаты

Pt := ScreenToClient(Point(Msg.XPos, Msg.YPos));

// Проверяем координаты на попадание в регионы стрелок

if PtInRegion(ArrowTopLeft, Pt.X, Pt.Y) then

Msg.Result := HTTOPLEFT

else if PtInRegion(ArrowTopRight, Pt.X, Pt.Y) then

Msg.Result := HTTOPRIGHT

else

if PtInRegion(ArrowBottomLeft, Pt.X, Pt.Y) then

Msg.Result := HTBOTTOMLEFT

else

if PtInRegion(ArrowBottomRight, Pt.X, Pt.Y) then

Msg.Result := HTBOTTOMRIGHT;

end;

Вот и все. С помощью нескольких нехитрых приемов мы получили окно, которое имеет такой необычный вид (см. рис. 1.14).

GDI позволяет рисовать линии разных стилей, но бывают ситуации, когда стандартных возможностей по изменению стиля линий не хватает. В этом разделе мы покажем, как рисовать линии произвольного стиля (начнем с прямых, потом перейдем к кривым Безье), а также сделаем "резиновую" линию, которую пользователь может тянуть мышью.

Рисование нестандартных линий выполняется следующим образом: вычисляются координаты всех пикселов, составляющих данную прямую, а потом каждый из них (а при необходимости — и какая-либо его окрестность) раскрашиваются нужным цветом. Следовательно, возникает вопрос об определении координат пикселов.

Существует ряд алгоритмов вычисления этих координат. Наиболее известный из них — алгоритм Брезенхэма (Bresengham), который заключается в равномерном разбрасывании "ступенек" разной длины вдоль линии. В Windows используется алгоритм GIQ (Grid Intersection Quantization). Каждый пиксел окружается воображаемым ромбом из четырех пикселов. Если прямая имеет общие точки с этим ромбом, то пиксел рисуется.

Самостоятельно реализовывать один из таких алгоритмов нет необходимости — в Windows существует функция LineDDA, которая возвращает вызвавшей ее программе координаты линии. Эта функция в качестве параметра принимает координаты начала и конца линии, а также указатель на функцию, которой будут передаваться координаты пикселов. Данная функция должна быть реализована в программе. За время выполнения LineDDAэта функция будет вызвана столько раз, сколько пикселов содержит линия (как обычно в Windows, последний пиксел не считается принадлежащим прямой). Каждый раз при вызове ей будут передаваться координаты очередного пиксела, причем пикселы будут упорядочены от начала к концу прямой.

В примере Lines (рис. 1.15) с помощью LineDDAрисуется пять различных типов линий. Рассмотрим на примере самого сложного из реализуемых программой типов линии ("Зеленая елочка"), как это делается (листинг 1.58).

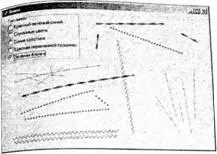
Рис. 1.15. Окно программы Lines

// константы для типа "Зеленая елочка"

const

// Угол отклонения "иголки" от направления линии

FirNeedleAngle = 30;

//Длина иголки

FirNeedleLength = 8;

var

Counter: Integer; // Счетчик точек линии

// Вспомогательные переменные для построения "елочки"

DX1, DY1, DX2, DY2: Integer;

// Линия в виде "елочки"

procedure LineDrawFir(X, Y: Integer; Canvas: TCanvas); stdcall;

begin

with Canvas do case Counter mod 10 of

0: begin

MoveTo(X, Y);

LineTo(X + DX1, Y + DY1);

end;

5:

begin

MoveTo(X, Y);

LineTo(X + DX2, Y + DY2);

end;

end;

Inc(Counter);

end;

procedure TLinesForm.Line(X1, Y1, X2, Y2: Integer);

var

Angle: Extended;

begin

case RGroupLine.ItemIndex of

...

4:

begin

Counter := 0;

Angle := ArcTan2(Y2 - Y1, X2 - X1);

DX1 := Round(FirNeedleLength *

Cos(Angle + Pi / 180 * FirNeedleAngle));

DY1 := Round(FirNeedleLength *

Sin(Angle + Pi / 180 * FirNeedleAngle));

DX2 := Round(FirNeedleLength *

Cos(Angle - Pi / 180 * FirNeedleAngle));

DY2 := Round(FirNeedleLength *

Sin(Angle - Pi / 180 * FirNeedleAngle));

LineDDA(X1, Y1, X2, Y2, @LineDrawFir, Integer(Canvas));

end;

end;

end;

Каждая "иголка" — это линия длиной FirNeedleLengthпикселов, отклоняющаяся от направления прямой на угол FirNeedleAngleградусов. "Иголки" отклоняются попеременно то в одну, то в другую сторону от прямой. В процедуре Lineсначала рассчитываются смещения координат конца "иголки" относительно начала и результаты помещаются в глобальные переменные DX1, DY1, DX2, DY2. Переменная Counterслужит для определения номера точки. Перед вызовом LineDDAона инициализируется нулем. Затем вызывается функция LineDDA, в качестве одного из параметров которой передается указатель на функцию обратного вызова LineDrawFir. В результате этого функция LineDrawFirбудет вызвана последовательно для каждого из пикселов, составляющих линию, начиная с (X1, Y1). LineDrawFirведет подсчет пикселов, каждый раз увеличивая Counterна единицу. Если остаток от деления номера точки на 10 равен 0, рисуется "иголка", отклоняющаяся в положительном направлении, если 5 — в отрицательном. В остальных случаях не рисуется ничего. Так получается "елочка".

Теперь нужно дать пользователю возможность рисовать линии. Для этого мы используем стандартную "резиновую" линию: пользователь нажимает левую кнопку мыши и, удерживая ее, передвигает мышь. До тех пор, пока кнопка удерживается, за курсором тянется линия. Как только пользователь отпускает кнопку, линия "впечатывается" в рисунок.

Сама по себе реализация "резиновой" линии очень проста: при наступлении события OnMouseDownзапоминаются координаты начала линии и взводится флаг, показывающий, что включен режим рисования "резиновой" линии. Также запоминаются координаты конца отрезка, который на данный момент совпадает с началом. В обработчике OnMouseMove, если включен режим рисования "резиновой" линии, стирается линия со старыми координатами конца и рисуется с новыми. При наступлении OnMouseUpпрограмма выходит из режима рисования "резиновой" линии, рисуя окончательный ее вариант с текущими координатами конца.

Самое сложное в этой последовательности действий — стереть нарисованную ранее линию. Если бы у нас был однородный фон, можно было бы просто нарисовать старую линию еще раз цветом фона — это выглядело бы как ее стирание. Но поскольку фон не однородный, а составлен из нарисованных ранее линий, этот способ мы применить не можем.