А. Григорьев - О чём не пишут в книгах по Delphi

Для решения этой задачи мы здесь рассмотрим самый простой метод — инверсное рисование (более сложный метод будет рассмотрен чуть позже). При этом каждая точка, принадлежащая линии, закрашивается не каким-либо фиксированным цветом, а инвертируется (т.е. к текущему цвету точки применяется операция not). Для стирания линии просто рисуем ее еще раз: двойная инверсия восстанавливает предыдущий цвет точек ( not not X = Xдля любого X).

При рисовании пером и кистью GDI позволяет использовать различные растровые операции , которые определяют результирующий цвет каждого пиксела в зависимости от цвета фона и пера или кисти. По умолчанию применяется операция R2_COPYPEN, в которой цвет фона игнорируется, а результирующий цвет пиксела совпадает с цветом пера или кисти. Изменить растровую операцию можно с помощью функции SetROP2(двойка в названии функции показывает, что устанавливаемая растровая операция имеет два аргумента — цвет рисования и цвет фона: при выводе растровых рисунков могут применяться растровые операции с тремя аргументами — см. функцию BitBlt). Нас будет интересовать операция R2_NOT, которая инвертирует фоновый цвет, игнорируя цвет пера или кисти.

Растровая операция влияет на все, что рисуется с помощью пера и кисти, т.е. на рисование границ фигур и их заливку. Кроме того, растровая операция влияет также на результат работы функции SetPixel(и, соответственно, изменение цвета с помощью Canvas.Pixels[X, Y]), т.к. эта операция выполняется с мощью кистей.

Код, рисующий "резиновую" линию, приведен в листинге 1.59.

procedure TLinesForm.FormMouseDown(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X, Y: Integer);

begin

if Button = mbLeft then begin

OldX := X;

OldY := Y;

BegX := X;

BegY := Y;

LineDrawing := True;

end;

end;

procedure TLinesForm.FormMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer);

begin

if LineDrawing and ((X <> OldX) or (Y <> OldY)) then

with Canvas do

begin

SetROP2(Handle, R2_NOT);

Line(BegX, BegY, OldX, OldY); // Стираем старую линию.

Line(BegX, BegY, X, Y); // Рисуем новую.

OldX := X;

OldY := Y;

end;

end;

procedure TLinesFom.FormMouseUp(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X, Y: Integer);

begin

if (Button = mbLeft) and LineDrawing then

begin

case RGroupLine.ItemIndex of

2: Canvas.Pen.Color := clBlue;

3: begin

Canvas.Brush.Color := clRed;

Canvas.Pen.Color := clRed;

end;

4: Canvas.Pen.Color := clGreen;

end;

Line(BegX, BegY, X, Y);

LineDrawing := False;

end;

end;

Обратите внимание, что резиновая линия следует за мышью даже тогда, когда мышь выходит за пределы формы, т.е. форма получает сообщения мыши, когда курсор находится за ее пределами. Это становится возможным благодаря захвату мыши окном. Любое окно в Windows может захватить мышь для монопольного использования, и тогда все сообщения от мыши будет получать это окно, независимо от того, где находится курсор. В VCL любой визуальный компонент, у которого установлен стиль csCaptureMouse(а у формы он по умолчанию установлен) автоматически захватывает мышь при нажатии левой кнопки и освобождает при ее отпускании, поэтому мы получаем требуемый нам эффект автоматически.

Сделаем следующий шаг — научимся рисовать произвольным стилем не только прямые, но и кривые. Проще всего это сделать с так называемыми кривыми Безье — они, во-первых, поддерживаются системой Windows, а во-вторых, ими можно аппроксимировать многие другие кривые (в частности, в Windows NT/2000 XP все кривые — окружности, эллипсы, дуги — аппроксимируются кривыми Безье).

Теорию кривых Безье разработал П. де Кастело в 1959 году и, независимо от него, П. Безье в 1962 году. Для построения кривой Безье N -го порядка необходимо N +1 точек, две из которых определяют концы кривой, а остальные N -1 называются опорными. В компьютерной графике наибольшее распространение получили квадратичные кривые Безье, строящиеся по трем точкам, и кубические кривые Безье, строящиеся по четырем точкам. Квадратичные кривые Безье используются, например, в шрифтах TrueType при определении контуров символов. Windows API позволяет строить только кубические кривые Безье.

Кубические кривые Безье задаются следующей формулой:

P(t) = А(1-t)³ + 3Bt(1-t)² + 3Ct²(1-t)+Dt³ (1)

где А — начало кривой, D — ее конец, а В и С — первая и вторая опорные точки. Прямая АВ касательная к кривой в точке А , прямая CD — в точке D . Параметр t изменяется от 0 до 1. При t = 0 P(t) = А , при t = 1 P(t) = D.

Одним из важнейших свойств кривой Безье является ее делимость. Если кривую разделить на две кривых в точке t = 0,5, каждая из полученных кривых также будет являться кривой Безье. На этом свойстве основывается алгоритм рисования кривых Безье: если кривая может быть достаточно точно аппроксимирована прямой, рисуется отрезок прямой, если нет — она разбивается на две кривых Безье, к каждой из которых вновь применяется этот алгоритм. Для рисования кривых Безье служат функции PolyBezier, PolyBezierToи PolyDraw.

В некоторых случаях удобно строить кривую Безье не по опорным точкам, а по точкам, через которые она должна пройти. Пусть кривая начинается в точке А, при t =⅓ проходит через точку В' , при t =⅔ — через точку С' , и заканчивается в точке D. Подставляя эти точки в уравнение (1), получаем систему, связывающую В' и С' с В и С . Решая систему, получаем

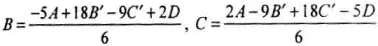(2)

Из этих уравнений, в частности, следует, что для любых четырех точек плоскости существует, и притом единственная, кривая Безье, которая начинается в первой точке, проходит при t =⅓ через вторую точку, при t =⅔ — через третью и завершается в четвертой точке. Аналогичным образом можно вычислить опорные точки для кривой, которая должна проходить через заданные точки при других значениях t .

API Windows реализует поддержку специфических объектов, называемых траекториями (path). Траектория представляет собой запись движения пера и включает один или несколько замкнутых контуров. Каждый контур состоит из отрезков прямых и кривых Безье. Для построения траектории в Windows NT/2000/XP могут быть задействованы все графические функции рисования прямых, кривых и замкнутых контуров, а также функции вывода текста (в этом случае замкнутые контуры будут совпадать с контурами символов). В Windows 9x/Me могут быть использованы только функции рисования прямых, ломаных, многоугольников (за исключением PolyDrawи Rectangle), кривых Безье и функций вывода текста. Функции рисования эллипсов, окружностей и эллиптических дуг не могут быть использованы для создания траектории в Windows 9x/Me, т.к. в этих системах эллиптические кривые рисуются специальным алгоритмом, а не аппроксимируются кривыми Безье. Для создания траектории предусмотрены функции BeginPathи EndPath. Все вызовы графических функций, расположенные между BeginPathи EndPath, вместо вывода в контекст устройства будут создавать в нем траекторию.