Генри Нив - Организация как система. Принципы построения устойчивого бизнеса Эдвардса Деминга

«Все было чудесно, за исключением того, что аппарат не делал копий. А вообще-то все было в полном порядке».

График функции потерь Тагути, показанный на рисунке 34, – это парабола, вытянутая вдоль вертикальной оси и имеющая минимальное значение, равное нулю, в точке номинального значения показателя качества. Уравнение такой параболы имеет вид:

где: х – измеряемое значение показателя качества; х 0 – его номинальное значение; L ( x ) – значение функции потерь Тагути в точке х; с – коэффициент масштаба (подбираемый в соответствии с используемой денежной единицей при измерении потерь). Это наиболее естественная и простая математическая функция, пригодная для представления основных особенностей функции потерь Тагути, рассмотренных в главе 11 [53]. Конечно, это не означает, что такой ее вид – наилучший выбор в каждом конкретном случае ее применения. Отметим, например, тот факт, что вышеприведенная формула предполагает одинаковый уровень потерь при отклонениях от номинала в обе стороны (в конце предшествующей главы мы рассматривали конкретный случай, когда это предположение не выполняется). С другой стороны, хотя данная модель часто служит разумным приближением для показателя качества в пределах его допусков и на не слишком большом удалении от границ допуска, она, очевидно, не подходит для больших отклонений от номинального значения. Однако наши процессы не столь уж плохи, чтобы нам требовалось рассматривать такие значительные отклонения.

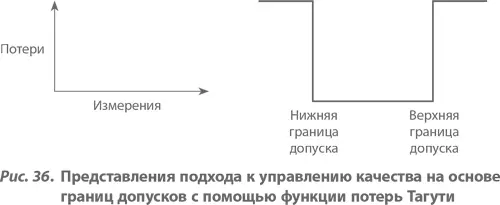
Но даже если наша параболическая модель и не вполне корректна, она, без сомнения, значительно ближе к действительности, чем функция потерь, соответствующая подходу к качеству на основе установления границ допусков, представленная на рисунке 36. Последняя модель предполагает, что потери отсутствуют при всех отклонениях от номинала в пределах допусков, но они скачкообразно возникают на границах поля допуска. С учетом проведенного в предшествующей главе обсуждения здесь не нет нужды в детальном рассмотрении данного вопроса, за исключением одного аспекта. Припомните сделанное нами в главе 11 наблюдение об осознании важности допусков. В любой системе, механической или бюрократической, которая спохватывается, только когда что-либо выходит за границы допусков, скоропалительные действия оказываются весьма дорогостоящими. Значит, в подобных случаях действительно имеется резкое увеличение потерь после выхода показателя качества за границы допусков, но эти потери обусловлены самой системой управления, а не возникают в результате отклонений уровня качества самой продукции или услуги.

Ниже мы воспользуемся параболической моделью для более детального изучения понятий и примеров, рассмотренных в главе 11. Поскольку это всего лишь модель, конкретные числа, получаемые в ходе расчетов, не так уж важны. Поэтому незначительные отличия в числах не будут рассматриваться как что-то значимое. Стратегия, дающая несколько большие потери, чем другая стратегия в предположении применимости этой модели, при замене этой модели на другую может оказаться более предпочтительной для функции потерь. Но когда мы обнаруживаем различия на целые порядки (например, когда потери от одной стратегии в 10, 50 или даже 100 раз превышают потери от другой), мы можем с полной уверенностью сказать, что различия в стратегиях весьма значительны, даже с учетом того, что параболическая модель – всего лишь идеализация.

В качестве дальнейшей идеализации, которая нужна для проведения численных сравнений в данной главе, мы вынуждены предположить, что рассматриваемые здесь процессы будут абсолютно стабильными. Приведенный в главе 4 термин «абсолютно стабильный» предполагает, что статистическое распределение процесса неизменно, не колеблется. В частности, это означает, что мы можем говорить в терминах истинных значений для среднего и стандартного отклонения, которые мы обозначим (но только в данной главе) символами μ и σ соответственно. (Хотя это противоречит важному замечанию Деминга касательно реальных процессов; см.: «Выход из кризиса», стр. 293.)

Далее мы будем использовать понятие средних потерь Тагути. Средние потери Тагути, применительно к выборке или партии из n изделий, для которых значения х 1, х 2…, х n рассматриваемого показателя качества х равны:

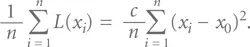
Если процесс абсолютно стабилен и имеет плотность распределения вероятности, тогда средние потери Тагути можно вычислить из:

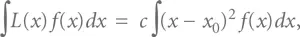
что соответствует площади под кривой, задаваемой произведением функции потерь L ( x ) на плотность вероятности f ( x ). Некоторые очевидные математические преобразования позволяют привести это выражение к виду:

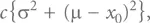
где члены внутри фигурных скобок ({…}) представляют соответственно квадратичное (стандартное) отклонение (обычно связанное с дисперсией) и квадрат смещения. Следует заметить, что средние потери Тагути не зависят каким-то сложным образом от f ( x ); их можно весьма просто вычислить, если известны простые параметры, входящие в последнее выражение [54].

Чтобы облегчить сравнения, давайте также введем обозначение для воспроизводимости процесса. В разных компаниях она определяется различным образом, но мы будем полагать ее равной разности между верхней и нижней границами допуска деленной на разность между верхней и нижней естественными пределами процесса, где для естественных пределов процесса мы используем «истинные» границы 3σ для индивидуальных наблюдений, так что знаменатель можно представить просто как 6σ [55].

Воспроизводимость, равная 1 ( единичная воспроизводимость), соответствует процессу, который в большинстве случаев едва укладывается в границы допусков [56]. Процесс иногда называют воспроизводимым или невоспроизводимым в зависимости от того, превосходит ли показатель воспроизводимости единицу или нет. Обычный образ мыслей на Западе – признание значения 1 1/3 как соответствующего исключительно эффективному процессу, а значения 1 2/3 – уже, возможно, слишком экстравагантным, поскольку вероятность получения в этом случае измерения за пределами допусков оказывается пренебрежимо малой [57]. Однако заметим, что данные о процессах из японской практики, упоминаемые в главе 11, позволяют оценить их уровень воспроизводимости от 3 до 5. И чтобы мера воспроизводимости отражала то, что процесс может давать на самом деле (а не то, на что он потенциально способен), надо предположить, что процесс точно настроен (центрирован), т. е. среднее процесса совпадает с номинальным значением х 0. Ниже мы рассмотрим, что происходит, если это предположение не выполняется.