Генри Нив - Организация как система. Принципы построения устойчивого бизнеса Эдвардса Деминга

Мы должны выбрать значение масштабного коэффициента с в уравнении для параболы таким образом, чтобы процесс, имеющий воспроизводимость 1 и точно центрированный, имел бы средние потери Тагути, равные 100 единицам. Вначале рассмотрим значения средних потерь Тагути для абсолютно стабильного процесса, точно настроенного на номинальное значение х у, но в предположении различной воспроизводимости процесса.

Мы видим, что повышение воспроизводимости от 1 1/3 до 1 2/3 уменьшает средние потери Тагути от половины до трети их значения по сравнению с потерями, соответствующими единичной воспроизводимости. Однако повышение воспроизводимости до 3–5 дает огромный эффект, описываемый в терминах порядков величин, как мы говорили об этом ранее. Графики средних потерь Тагути, в зависимости от воспроизводимости процессов, для всех примеров, рассматриваемых в данной главе, показаны на рисунке 41.

Важность точной настройки (центрирования) процесса можно быстро оценить, сравнивая данные таблиц 1 и 2. Данные таблицы 2 рассчитаны в предположении, что процесс неточно настроен и центрирован в середине диапазона между номиналом и одним из пределов допуска.

Плохая настройка процесса полностью разрушает все потенциальные преимущества улучшения воспроизводимости. Однако даже при такой плохой настройке процесс, имеющий воспроизводимость 2 и выше, практически не будет давать изделий, выходящих за границы допусков. Поэтому, хотя такой процесс рассматривался бы как безусловно выдающийся с точки зрения удовлетворения заданных допусков, – рассмотренный с позиций функции потерь Тагути он, безусловно, намного хуже, чем точно настроенный процесс; например, для эффективности, равной 2, потери в таблице 2 в десять раз превышают потери, приводимые в таблице 1.

Теперь мы рассмотрим два примера, описанные в конце предшествующей главы. Сначала обратимся к проблеме износа инструмента. Припомним детали: первоначально процесс настроен так, чтобы результаты измерений были близки к верхней границе допуска (ВГД). Затем износ инструмента будет приводить к постепенному уменьшению значений; когда результаты начинают приближаться к нижней границе допуска (НГД), процесс останавливается и инструмент заменяется. Отметим, что воспроизводимость рассматриваемого процесса (без учета его дрейфа) должна быть больше 1, чтобы такую схему вообще можно было реализовать, иначе возможность для маневрирования просто отсутствовала бы. Для полноты картины ниже мы рассмотрели также случай, соответствующий единичной воспроизводимости.

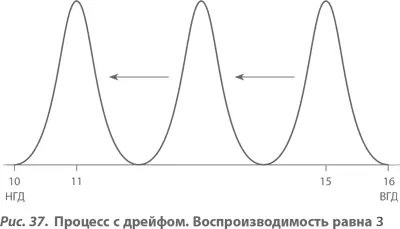
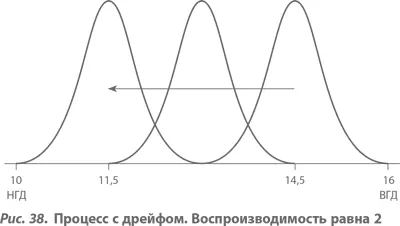
На рисунке 37 показан случай, когда воспроизводимость процесса равна 3. Для примера мы принимаем значения НГД и ВГД равными 10 и 16 соответственно, а стандартное отклонение σ – равным 1/3 (если бы σ была равна 1, то воспроизводимость процесса также была бы равна единице). Первоначально мы настраиваем центр распределения на 15, так что распределение попадает как раз ниже ВГД. Предположим, что среднее процесса с постоянной скоростью смещается вниз, к значению 11, и в этот самый момент мы останавливаем процесс, меняем инструмент и вновь настраиваем его на 15. (Если бы эффективность процесса была 2 вместо 3, т. е. σ = 0,5, тогда мы были бы должны первоначально установить центр процесса на 14,5 и позволить ему затем смещаться вниз, до 11,5, когда пора заменять инструмент. Этот случай представлен на рисунке 38.) Средние потери Тагути для процессов с различной воспроизводимостью, которыми «управляют» таким образом, представлены в таблице 3а. (При этом стоимость замены инструмента в явном виде при расчетах не учитывалась.)

Но что за сюрприз! Для малых значений воспроизводимости потери Тагути вначале уменьшаются, но вскоре начинают увеличиваться, так что потери для процесса с воспроизводимостью 5 оказываются более чем в два раза бо́льшими, чем для процесса с воспроизводимостью, равной 1! По здравом размышлении причина такого увеличения становится ясной. Когда воспроизводимость процесса велика, его первоначальная настройка дает значения, очень близкие к ВГД, таким образом, он принужден давать изделия с параметрами, сильно отличающимися от номинальных, что соответственно приводит к высоким потерям Тагути. То же справедливо, когда процесс уже сместился к НГД в моменты, непосредственно предшествующие смене инструмента. Вследствие квадратичного характера функции потерь ущерб, вызванный этими экстремальными ситуациями, превышает выгоды от получения хороших изделий в моменты, когда процесс находился вблизи номинального значения, на полпути от ВГД к НГД.

Отметим, что полученный вывод находится в прямом противоречии с миром, основанным на использовании модели соответствия требованиям допусков. Сама схема организована таким образом, чтобы вне зависимости от того, какова воспроизводимость процесса (коль скоро она превышает 1), не производилось бы продукции, выходящей за границы допусков. Увеличение показателя воспроизводимости процесса с этой точки зрения имеет то положительное следствие, что процесс может длиться дольше до момента, когда возникает потребность в замене инструмента. Однако, как мы теперь видим, эта выгода ложна с точки зрения потерь Тагути. Средние потери Тагути существенно снизятся, если мы сможем, например, менять инструмент в два раза чаще. Так, для процесса с воспроизводимостью 3 это позволит настроить его первоначально на 14 (а не на 15) и заменить его, когда среднее значение снизится до 12 (а не до 11). Средние потери Тагути будут в этом случае равны 44 вместо 144, хотя это все еще и близко не подходит к результату, который дает процесс с воспроизводимостью 3 без смещения (в этом случае, в соответствии с таблицей 1, средние потери Тагути равны 11). В то же время это существенное улучшение по сравнению с тем, что получается, если мы ждем до возможного предела, прежде чем сменить инструмент. Таблица 3Б показывает результат в два раза более частой смены инструмента для тех же значений воспроизводимости, что в таблице 3а.

Стоит ли существенное уменьшение средних потерь Тагути по сравнению с потерями, соответствующими в таблице 3а, тех дополнительных затрат, которые возникают из-за в два раза более частой замены инструмента? На этот вопрос должен дать ответ тот, кто руководит системой.