Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

В том, что число π появляется в площадях и длинах всех кругообразных объектов, рассмотренных нами, ничего удивительного нет. Но только этим сфера его влияния не ограничивается – оно обнаруживается даже там, где, казалось бы, ему делать совершенно нечего.

Возьмем для примера множество n ! подробно рассмотренное нами в главе 4. Казалось бы, причем тут окружности, эллипсы и прочие подобные фигуры и объекты – ведь оно нужно исключительно для того, чтобы подсчитывать дискретные величины. Мы знаем, что значение его вырастает стремительно, причем настолько, что до сих пор нет ни одного более или менее удобного и легкого способа его просчитать. Например, чтобы вычислить значение 100 000! нам потребуется несколько тысяч операций умножения. И все-таки один способ есть – столь же хитрый, сколь и полезный. Основан он на формуле Стирлинга, которая выглядит как

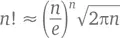
и в которой e = 2,71828… ( e – это еще одно важное иррациональное число, которое ждет вашего внимания в главе 10). Компьютер может подсчитать это до четырех значащих цифр – например, 64! = 1,269 × 10 89. А согласно формуле Стирлинга, 64! ≈ (64/ e ) 64√( 128π ) = 1,267 × 10 89. (Есть ли легкий способ возвести число в 64-ю степень? Да, есть! Поскольку 64 = 2 6, нам нужно взять 64/ e и возвести его в квадрат шесть раз.)

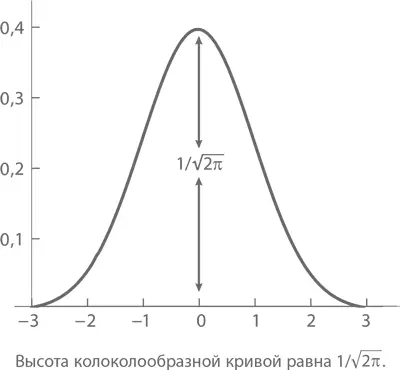
Знаменитая колоколообразная (или гауссова ) кривая , активно использующаяся в статистических исследованиях и некоторых экспериментальных науках, имеет высоту 1/√( 2π ) (подробнее о ней – в главе 10).

Встречается число π и в бесконечных суммах: как впервые наглядно показал Леонард Эйлер, сложение квадратов обратных величин положительных целых значений дает нам

А если мы повторно возведем в квадрат каждое из значений выше, сумма обратных величин четвертой степени окажется равной

Формулу эту можно обобщить, распространив на любой ряд обратных величин всех четных степеней основания числа 2 k . В ответе будет фигурировать π 2 k , умноженное на рациональное число.

А что насчет нечетных обратных величин? В главе 12 мы увидим, что сумма обратных величин положительных значений бесконечна. При любой нечетной степени больше 1 получим что-то наподобие этого:

(это пример для кубов). Сумма здесь будет, по идее, конечной, вот только простой формулы для ее точного вычисления пока никто не нашел.

Невероятно, но факт: π всплывает даже в задачах, связанных с вероятностью. Например, если вы выберете два случайных больших числа, вероятность того, что у них не будет ни одного общего простого множителя, составит чуть больше 60 %. Это приблизительно. А если точно, то 6/π² = 0,6079…. И то, что этот результат является обратной величиной для одной из посчитанных нами чуть выше бесконечных сумм – вовсе не совпадение.

К тому, что число π немного превышает 3, вы вполне можете прийти самостоятельно – для этого достаточно просто аккуратно все подсчитать. Но сначала нужно найти ответы на парочку вопросов. Во-первых, можно ли доказать соседство π и 3, не проводя специальных измерений? Во-вторых, существует ли для π какое-нибудь более удобоваримое представление (скажем, формула или простая дробь)?

На первый вопрос можно ответить, нарисовав окружность с радиусом 1, площадь который, как нам уже известно, равна π1² = π. На рисунке чуть ниже этот круг вписан в квадрат с длиной сторон, равной 2. Так как площадь квадрата очевидно больше площади круга, получаем, что π должно быть меньше 4.

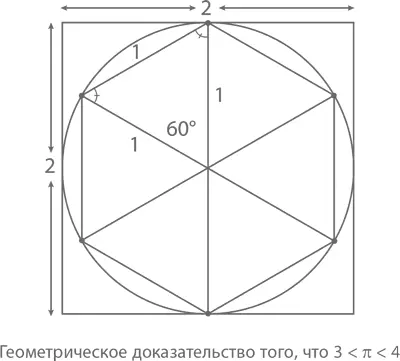
С другой стороны, в круг можно вписать шестиугольник – так, чтобы все шесть его вершин были расположены на окружности, причем на равном расстоянии друг от друга. Каким будет периметр этого шестиугольника? Разобьем его на шесть треугольников, величина центрального угла каждого из которых составит 360°/6 = 60°, а две стороны будут радиусами круга с длиной, равной 1 (что говорит о том, что все эти треугольники – равнобедренные). Согласно теореме о равнобедренных треугольниках, оставшиеся два угла должны быть равны между собой, то есть величина каждого составит 120°/2 = 60° – так мы узнаем, что треугольники не просто равнобедренные, но еще и равносторонние – с длиной сторон 1. Значит, площадь шестиугольника равна 6. А так как она должна быть меньше длины окружности в 2π (потому что круг очевидно больше шестиугольника), получаем 6 < 2π и π > 3. Так мы и приходим к желаемому

Можно на этом не останавливаться и попытаться еще сильнее сократить возможный разброс – для этого нам понадобятся полигоны с бóльшим количеством сторон. Так, если мы окружим единичный круг не квадратом, а шестиугольником, у нас получится доказать, что π < 2√ 3 = 3,46….

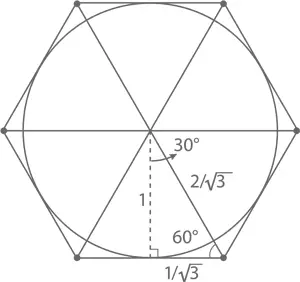
Еще раз: шестиугольник можно разделить на 6 равносторонних треугольников, каждый из них в свою очередь разбивается на 2 прямоугольных. Если длина меньшего катета равна x , длина гипотенузы составит 2 x . По теореме Пифагора x ² + 1 = (2 x )². Поиски x приводят нас к x = 1/√ 3 . Значит, периметр шестиугольника составит 12/√ 3 = 4√ 3 , а так как он должен быть больше длины окружности (2π ) , то π должно быть меньше 2√ 3 (смотрите-ка, мы пришли к тому же заключению, что и при сравнении площади окружности с площадью шестиугольника).

Следуя той же логике чередования «вписанных» и «описывающих» полигонов, состоящих последовательно из 12, 24, 48 и 96 сторон, один из величайших древнегреческих математиков Архимед сумел доказать, что 3,14103 < π < 3,14271, что сводится к немногим более простой формуле

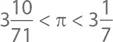
Есть несколько простых дробей, которые более-менее соотносятся со значением π. Например,

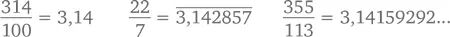
Лично мне больше всего нравится последняя. И не только потому, что она совпадает с π в 6 из всего множества знаков после запятой, но и потому, что использует первые три нечетных числа (причем по два раза и по порядку!): две единицы, две тройки и две пятерки.