Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Возьмем другой знакочередующийся ряд:

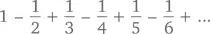
После четвертого члена нам становится понятно, что бесконечная сумма составит минимум 1 – 1/2 + 1/3 – 1/4 = 7/12 = 0,583…, после пятого – максимум 1 – 1/2 + 1/3 – 1/4 + 1/5 = 47/60 = 0,783…. Истина, как всегда, кроется где-то посередине – 0,693147…. С помощью исчисления мы можем найти действительное значение этого числа.

Чтобы размяться, возьмем следующий ряд

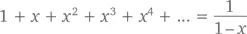
и посмотрим, что будет, если продифференцировать обе его части. Помните, в главе 11 мы определили, что производные 1, x, x 2, x 3, x 4и т. д. равны соответственно 0, 1, 2 x , 3 x 2, 4 x 3и т. д.? Получается, что производная бесконечной суммы есть (бесконечная) сумма производных. А теперь применим цепное правило, чтобы продифференцировать (1– x ) –1. При –1 < x < 1 получаем

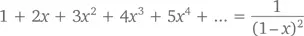
Посмотрим на другой ряд, заменив x на – x . При –1 < x < 1

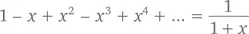
Найдем для обеих сторон антипроизводные (или первообразные ), то есть займемся тем, что называется интеграцией . Чтобы это сделать, двинемся назад: например, если производная x ² – 2 x , то первообразная 2 x – x ². (Специально для тех, кто любит «погорячее»: производная x ² + 5, x ² + π или x ² + c при любом значении c также равна 2 x , поэтому первообразная 2 x – и на самом деле x ² + c .) Значит, первообразными 1, x, x ², x ³, x 4и т. д. будут соответственно x, x 2/2, x 3/3, x 4/4, x 5/5 и т. д., а первообразной 1/(1 + x ) – натуральный логарифм 1 + x . То есть при –1 < x < 1

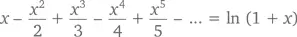
(Постоянная величина слева – 0, потому что при x = 0 нам нужно, чтобы левая часть соответствовала ln 1 = 0.) Так как x стремится к единице, мы получаем натуральное значение 0,693147…, а именно

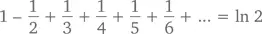
Если же заменить x на – x ², то при значении x , находящемся между –1 и 1,

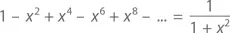
В большинстве учебников по исчислению сказано, что y = tan–1 x имеет производную Следовательно, если мы найдем первообразные обеих сторон (не забыв, что tan −10 = 0), то придем к

А положив x как величину, стремящуюся к нулю, – и к

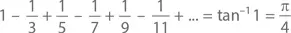
Правильно пользоваться геометрическим рядом мы уже научились. Почему бы немного не попользоваться им неправильно? Формула утверждает, что

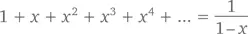
при любом значении x , ограниченным условием, что –1 < x < 1. А что, если набраться смелости и взять x = –1? Тогда наша формула примет следующий вид:

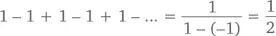
Конечно, это невозможно: при сложении и вычитании целых величин дробь вроде 1/2 просто не может образоваться, даже при сходящейся сумме. С другой стороны, крупица здравого смысла в таком ответе все-таки есть – просто взгляните на промежуточные суммы:

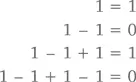
Возьмем другое «незаконное» значение – x = 2. Тогда ряд скажет нам, что

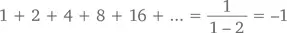
Этот ответ выглядит еще более нелепо, чем предыдущий: как может сумма положительных чисел быть отрицательной? Но зерно истины скрыто и здесь. Помните, в главе 3 мы разбирали случаи, когда положительная величина ведет себя как отрицательная в таких, например, отношениях:

Это привело нас к выводу, что 10 k ≡ (–1) k (mod 11).

А вот один очень интересный способ понять 1 + 2 + 4 + 8 + 16 +…, который потребует от нас нестандартного творческого подхода. Вернемся назад к главе 4, в которой мы выяснили, что любое целое может быть представлено в виде уникальной суммы двух степеней двойки. Именно этот принцип лежит в основе двоичной системы счисления – системы, благодаря которой современные компьютеры умеют считать. Причем количество степеней двойки обязательно конечно. Например, в 106 = 2 + 8 + 32 + 64 таких степеней всего четыре. Но предположим, что для нас вдруг стало доступно и бесконечное их количество. Типичное бесконечное целое выглядит как

где каждый член – это степень по основанию 2. К чему это нас приведет, пока неясно, но некоторая закономерность здесь уже прослеживается. Так, эти числа можно складывать, перенося лишние цифры в следующий разряд – как мы всегда и делаем. Например, прибавив к предыдущему ряду число 106, получим

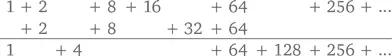
где две двойки предсказуемо дают 4, а две восьмерки – 16. А дальше смотрите, что происходит: этот результат мы прибавляем к следующим 16 и получаем 32. Плюс еще 32 – будет 64. А так как дальше у нас уже есть целых две величины, равные 64, имеем 64 и 128. Все, что выше 256, остается в единственном экземпляре. Теперь попробуйте представить, что произойдет, когда мы прибавим 1 к некой абстрактной «наибольшей» величине.

Мы получим бесконечную цепь реакций, уводящих за пределы уравнения все значения, не связанные степенными отношениями с 2. Следовательно, сумму вполне можно представить как 0. Так как (1 + 2 + 4 + 8 + 16 +…) + 1 = 0, вычитание 1 из обеих частей приведет нас к бесконечной сумме, ведущей себя в точности, как число –1.