Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

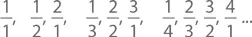
то есть мы берем дроби в соответствии с суммой их числителей и знаменателей. Так как любая рациональная величина неизбежно появляется в списке, их множество будет счетным.

А существуют ли вообще такие бесконечные множества, которые не являются счетными? Немецкий математик Георг Кантор (1845–1918) доказал, что все действительные величины, даже только те из них, что ограничены диапазоном от 0 до 1, образуют несчетное множество. Можно, конечно, попробовать перечислить их следующим образом:

и т. д. Но так мы никогда не выйдем за пределы величин с конечным количеством знаков. Число 1/3 = 0,333…, например, в нашем списке так и не встретится. Но, может, есть какой-нибудь другой, более эффективный способ перечисления? Кантор доказал, что его нет. Он пошел от обратного – предположил, что множество действительных величин является счетным. Он взял конкретный пример и начал с

Доказать, что этот список не будет полным, можно, «придумав» такое действительное число, которое никогда в нем не появится. Можно взять, скажем, величину 0, r 1 r 2 r 3 r 4…, где r 1есть целое в интервале от 0 до 9, которое отличается от первого числа только первой цифрой (в нашем примере r 1≠ 3). Так же обстоит и с r 2: оно отличается от второго числа второй цифрой (у нас r 2≠ 7). И так далее. Таким образом у нас может получиться, скажем, 0,2674… – число, которое никогда не появится в списке, даже на миллионной позиции, потому что будет отличаться от нее миллионной цифрой. А значит, какой бы список вы ни создавали, всегда будут такие величины, которые в нем не появятся, следовательно, множество действительных чисел является несчетным.

Эта схема известна под названием «канторовский диагональный процесс», но мне больше по душе «доказательство через кантор-аргумент» (кхм, прошу прощения).

По сути, мы только что показали, что, несмотря на бесконечность рациональных величин, величин иррациональных все же больше. Просто выберите случайное действительное значение, лежащее на оси, и оно почти наверняка окажется иррациональным.

Бесконечные ряды очень часто появляются при решении задач, связанных с вероятностью. Предположим, что вы кидаете два шестигранных кубика, причем кидаете до тех пор, пока в сумме у вас не выпадет 6 или 7. Если 6 выпадает раньше 7, вы выиграли, если наоборот – проиграли. Каковы ваши шансы на победу? Количество возможных комбинаций равно 6 × 6 = 36. Пять из них дают в сумме 6 (а именно (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)), шесть – 7 ((1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)). Следовательно, ваши шансы на победу составляют меньше 50 %. Но сколько именно? Всего значимых для вас комбинаций 5 + 6 = 11, в остальных случаях кубики придется бросать вновь. Из этих одиннадцати пять приведут вас к выигрышу, шесть – к поражению. Значит, ваши шансы равны 5/11.

К тому же ответу можно прийти и с помощью геометрического ряда. Шансы на выигрыш при первом броске равны 5/36. А при втором? Чтобы он вообще состоялся, при первом броске вам надо выбрость что-то, кроме 6 или 7. Не забываем, что оптимальный для нас результат – 6. Общая вероятность выбросить 6 или 7 при первом броске – 5/36 + 6/36 = 11/36, выбросить другую комбинацию – 25/36. Чтобы определить вероятность выигрыша при втором броске, умножим это число на вероятность выбросить 6 при любом броске – 5/36, – в результате получим (25/36)(5/36). Для третьего броска получим уже (25/36)(25/36)(5/36), для четвертого – (25/36)³(5/36) и т. д. Сложив все вместе, получим

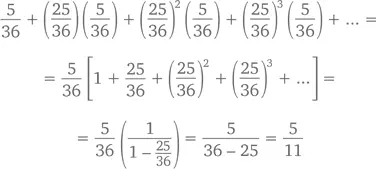
что и требовалось доказать.◻

Когда бесконечный ряд приводит нас к (конечной) сумме, мы говорим, что сумма сходится к этому значению. Когда же этого не происходит, мы говорим, что ряд расходится. Если ряд сходится, то отдельные его значения должны суммироваться до величин, стремящихся к 0. Например, ряд 1 + 1/2 + 1/4 + 1/8 +… сходится к 2, а значит, его члены 1, 1/2, 1/4, 1/8… все ближе подходят к 0.

Обратное же высказывание будет неверным, потому стремление каждого последующего члена ряда к 0 не есть гарантия того, что он не разойдется. Самый важный пример этого утверждения – гармонический ряд, названный так еще древними греками, обнаружившими, что струны лиры, соотносящиеся по длине, как 1, 1/2, 1/3, 1/4, 1/5…, издают гармоничные созвучия.

Теорема:Гармонический ряд является расходящимся, то есть

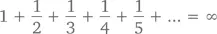
Доказательство:Прежде чем доказывать, что сумма этого ряда равна бесконечности, покажем сначала, что это есть просто некое очень большое число. Для этого разобьем ряд на несколько частей на основании количества цифр в знаменателе. Обратите внимание, что, поскольку каждый из первых 9 членов больше 1/10, то

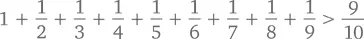
Каждый из следующих 90 членов больше 1/100, поэтому

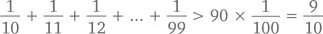
Аналогично поступим со следующими 900 членами (надо ли говорить, что каждый из них больше 1/1000?):

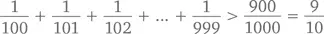
И так далее –

и тому подобное. Следовательно, сумма всех-всех членов равна как минимум

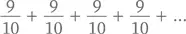
и так до бесконечности.

А вот забавный факт:

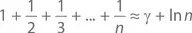
где γ есть число 0,5772155649…, так называемая постоянная Эйлера – Маскерони , а ln n – натуральный логарифм n , описанный нами в главе 10 (кстати, до сих пор доподлинно неизвестно, является ли число γ («гамма») рациональным или иррациональным). Аппроксимация будет тем точнее, чем больше будет значение n . А вот и таблица, в которой сумма ряда сопоставлена с аппроксимацией: