Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

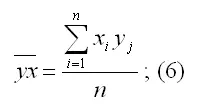
Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у . Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:

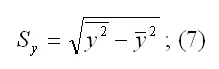
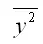
– среднее значение из квадратов значений зависимой переменной у:

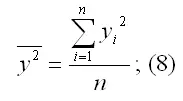
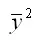
– квадрат средних значений зависимой переменной у:

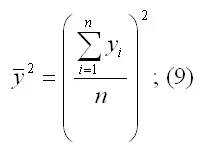
Sx – показатель выборочного среднеквадратического отклонения независимой переменной х . Этот показатель характеризует, на сколько единиц в среднем отклоняются значения независимой переменной х от её среднего значения. Они рассчитывается по формуле:

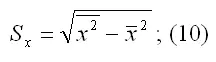
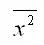
– среднее значение из квадратов значений независимой переменной х :

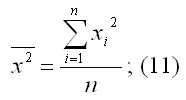
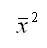
– квадрат средних значений независимой переменной х:

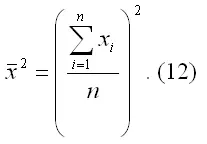
При использовании рассмотренного подхода оценивания неизвестных параметров линейной модели парной регрессии, следует учитывать что ryx=rxy, однако βyx≠βxy.

При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.

Несмещённой оценкой дисперсии(или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:

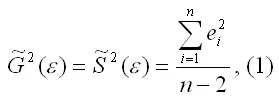
где n – это объём выборочной совокупности;

еi – остатки регрессионной модели:

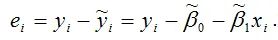
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:

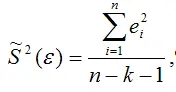
где k – число оцениваемых параметров модели регрессии.

Оценка матрицы ковариаций случайных ошибок Cov(ε) будет являться оценочная матрица ковариаций:

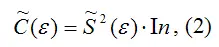
где I n – единичная матрица.

Оценка дисперсии случайной ошибки модели регрессии распределена по ε2 (хи-квадрат) закону распределения с (n-k-1) степенями свободы.

Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства

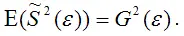
Доказательство. Примем без доказательства справедливость следующих равенств:

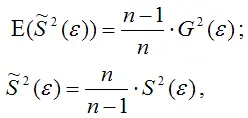
где G2(ε) – генеральная дисперсия случайной ошибки;

S2(ε) – выборочная дисперсия случайной ошибки;

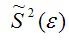
– выборочная оценка дисперсии случайной ошибки.

Тогда:

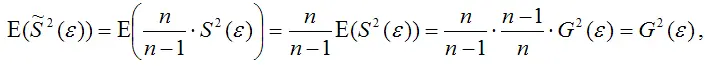
т. е.

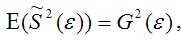
что и требовалось доказать.

Следовательно, выборочная оценка дисперсии случайной ошибки

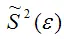
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(ε).

При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х , наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты β . Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.

Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки

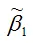
от величины случайной ошибки ε.

МНК-оценка коэффициента β1 модели регрессии определяется по формуле:

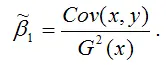
В связи с тем, что переменная у зависит от случайной компоненты ε (yi=β0+β1xi+εi), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:

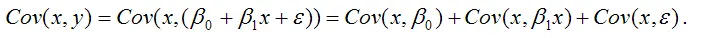
Для дальнейших преобразования используются свойства ковариации:

1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const ;

2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).

Исходя из указанных свойств ковариации, справедливы следующие равенства: