Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Cov(x,β0)=0 (β0=const);

Cov(x, β1x)= β1*Cov(x,x)= β1*G2(x).

Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:

Cov(x,y)= β1G2(x)+Cov(x,ε).

В результате МНК-оценка коэффициента β1 модели регрессии примет вид:

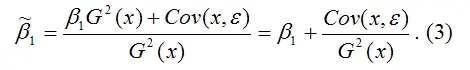
Таким образом, МНК-оценка

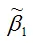
может быть представлена как сумма двух компонент:

1) константы β1 , т. е. истинного значения коэффициента;

2) случайной ошибки Cov(x,ε ), вызывающей вариацию коэффициента модели регрессии.

Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.

Аналогично доказывается, что МНК-оценка

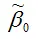
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки

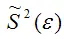
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ε.

Предположим, что методом наименьших квадратов получена оценка

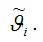
Для того, чтобы данная оценка могла быть принята за оценку параметра

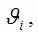
необходимо и достаточно выполнения трёх статистических свойств:

1) свойства несмещённости;

2) свойства состоятельности;

3) свойства эффективности.

Сделаем следующие предположения об отклонениях єi:

1) величина єi является случайной переменной;

2) математическое ожидание єi равно нулю: М ( єi ) = 0;

3) дисперсия є постоянна: D( єi ) = D( єi ) = s 2 для всех i, j;

4) значения єi независимы между собой, следовательно, справедливо следующее выражение:

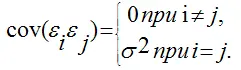
Если данные предпосылки выполняются, то оценки, найденные с помощью метода наименьших квадратов, обладают свойствами несмещённости, состоятельности и эффективности.

Если третье и четвёртое предположения не выполняются, т. е. дисперсия случайных компонент непостоянна и/или значения є коррелируют друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.

Величина

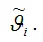
называется несмещённой оценкойпараметра

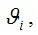
если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности:

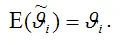
Отсюда следует, что

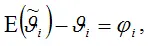
где φi – это величина смещения оценки.

Рассмотрим свойство несмещённости МНК-оценок на примере модели парной регрессии.

Необходимо доказать, что оценка

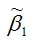
полученная методом наименьших квадратов, является несмещённой оценкой параметра β1 для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства

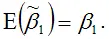
Доказательство. Проведём доказательство утверждения

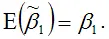
через ковариационную матрицу:

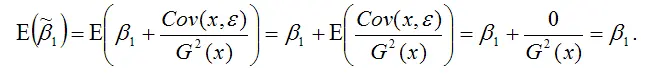
То же самое утверждение

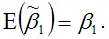
можно доказать в более развёрнутом виде:

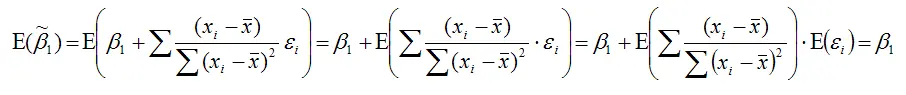
Следовательно, оценка

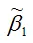
полученная методом наименьших квадратов, является несмещённой оценкой коэффициента β1 нормальной линейной модели парной регрессии.

Свойство несмещённости оценки

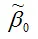
коэффициента β0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.

Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi , полученных методом наименьших квадратов, целесообразно провести в матричной форме:

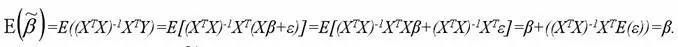
Следовательно, оценки

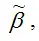
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βi нормальной линейной модели множественной регрессии.

Величина

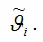
является состоятельной оценкой параметра

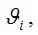
если она удовлетворяет закону больших чисел. Суть закона больших чисел состоит в том, что с увеличением выборочной совокупности значение оценки

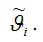
стремится к значению параметра

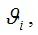
генеральной совокупности:

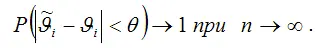
Условие состоятельности можно также записать через теорему Бернулли :

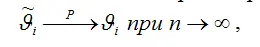
т. е. значение оценки

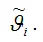
сходится по вероятности к значению параметра

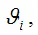
генеральной совокупности, при условии, что объём выборочной совокупности стремится к бесконечности.

На практике оценка