Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

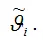
полученная методом наименьших квадратов, считается состоятельной оценкой параметра,

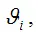
если выполняются два условия:

1) смещение оценки равно нулю или стремится к нему при объёме выборки, стремящемся к бесконечности:

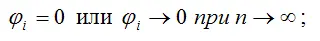
2) дисперсия оценки параметра

стремится к нулю при объёме выборки, стремящемся к бесконечности:

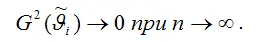
Рассмотрим свойство состоятельности МНК-оценок на примере модели парной регрессии.

Необходимо доказать, что оценка

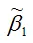
полученная методом наименьших квадратов, является состоятельной оценкой параметра β1 для нормальной линейной модели регрессии.

Доказательство. Докажем первое условие состоятельности для МНК-оценки

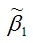
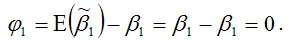
Докажем второе условие состоятельности для МНК-оценки

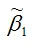
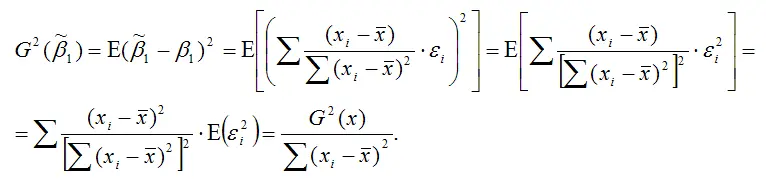
МНК-оценка

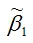
подчиняется нормальному закону распределения с математическим ожиданием β1 и дисперсией

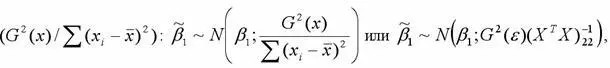
или

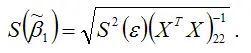
где индекс 22 указывает на расположение дисперсии параметра β1 в матрице ковариаций.

Свойство состоятельности оценки

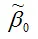
коэффициента β0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.

Оценка стандартной ошибки МНК-оценки

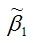
определяется по формуле:

Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi , полученных методом наименьших квадратов, целесообразно провести в матричной форме:

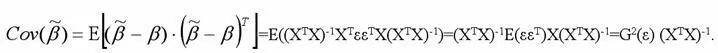
Следовательно, оценки

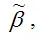
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βi нормальной линейной модели множественной регрессии.

Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова .

Свойство эффективности оценок неизвестных параметров модели регрессии, полученных методом наименьших квадратов, доказывается с помощью теоремы Гаусса-Маркова.

Сделаем следующие предположения о модели парной регрессии:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;

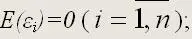
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

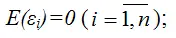
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;

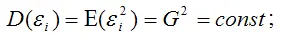
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

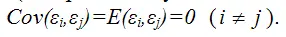
Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).

Если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0 и β1 .

Если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0…βn .

Для обозначения дисперсий МНК-оценок неизвестных параметров модели регрессии используется матрица ковариаций.

Матрицей ковариаций МНК-оценок параметров линейной модели парной регрессииназывается выражение вида:

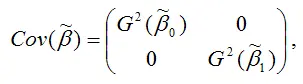
где

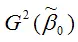
– дисперсия МНК-оценки параметра модели регрессии β0 ;

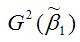
– дисперсия МНК-оценки параметра модели регрессии β1 .