Анатолий Молчанов - Население Земли как растущая иерархическая сеть

К степенному закону приводит сделанное Форстером и его коллегами фантастическое предположение о том, что коэффициент мирового естественного прироста на всем протяжении исторического процесса не был постоянен, как при экспоненциальном росте, а слабо зависел от численности: a = a 0N 1/k. (Такая зависимость могла бы иметь место, если в соответствии с теорией игр рассматривать растущее население Земли как некую коалицию, ведущую глобальную игру против сил природы.)

Важно понимать, что это предположение, сделанное благодаря модной в то время теории игр (спасибо ей за это!), расходящееся со здравым смыслом и требующее большой вычислительной работы – что было совсем не просто в 1960 году! – представляется совершенно фантастическим, если не безумным. Результат точно должен был получиться отрицательным, т. е. точность значений С, p и t 0должна была оказаться очень небольшой.

Но совершилось чудо – эта точность, с которой определились постоянные Форстера, совершенно неожиданно оказалась чрезвычайно высокой, можно даже сказать невозможно высокой, делающей гиперболу Форстера, по сути, предзаданной:

Результаты исследования Форстера и его коллег демографических данных по численности населения мира методом наименьших квадратов: N = C/(t 0– t) p; C = 179 ± 14 млрд; t 0= 2027 ± 5; p = 0,99 ± 0,009.

Здесь важно то, что показатель степенной функции, описывающей рост, практически равен единице, т. е. простейшему целочисленному значению. (При вычислении p по методу наименьших квадратов могло быть получено любое действительное число, например, p = 0,78 или p = 1,16, но вышло, что p = 1 с точностью до одного процента.)

Вряд ли целочисленность p является всего лишь делом случая. Такое совпадение возможно, но, очевидно, весьма маловероятно. Скорее всего, за этим стоит нечто большее, позволяющее считать население мира единой системой. И по причине этой «невозможно» высокой точности для p и t 0только и можно говорить о новой фундаментальной константе С, Форстера, характеризующей растущее человечество как систему. Стоит отметить, что сам Форстер, хотя и шутил на эту тему, но так и не понял ни причины, ни значения открытого им аномального гиперболического роста.

Немецкий физик Хорнер [35]расширил время действия закона Форстера до неолита, подключив дополнительные данные, что несколько увеличило постоянную Форстера С и оставило практически без изменения p и t 0[1]:

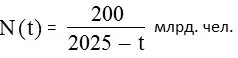
Рис. 1. Гипербола Хорнера.

Итак, в начале шестидесятых годов прошлого века была введена новая, видимо, фундаментальная постоянная, определяющая рост численности Homo sapiens и его эволюцию, смысл которой для ее первооткрывателя так и остался непонятым. Размерность этой эмпирической константы, как следует из формулы Форстера, – год в степени 0,99. Что позволяет предположить, что p = 1, и постоянная Форстера должна иметь размерность времени. Однако авторы статьи «Судный день. Пятница 13 ноября 2026 года» гипотезу о целочисленности p не рассматривали, что не позволило им определить С с максимально возможной точностью.

Действительно, значение C = 179 ± 14 млрд лет было получено в предположении о том, что показатель p является неопределенным и должен вычисляться по методу наименьших квадратов так же, как C и t 0. Что представляется вполне логичным. Но получив для него столь близкое к единице значение, Форстер и его коллеги должны были сделать перерасчет на основе тех же самых данных, которыми они располагали, полагая, что p = 1.

Этого сделано не было, и значение постоянной Форстера оказалось несколько заниженным. Далее мы приведем наши расчеты, которые позволяют уточнить значение постоянной С, приведенное в статье «Судный день. Пятница 13 ноября 2026 года». Эти расчеты хотя и не могут считаться вполне корректными, зато позволяет определить постоянную С при p = 1 на основе результатов, полученных Форстером и его коллегами: C = 188 ± 14 млрд лет. (Данные, использованные ими, опубликованы не были.)

Теперь мы вплотную подошли к вопросу о смысле постоянной Форстера. Что означают эти 188 миллиардов лет? – Непонятно… но уж только не численность народонаселения за год до сингулярности, т. к. до этого значения она точно не дорастет. Есть один интервал времени, известный из космологии, который по порядку величины близок к данной константе: это возраст Вселенной T = 13,8 млрд лет. Если постоянная Форстера С имеет космологический смысл и как-то связана с универсальной эволюцией, то ее отношение к возрасту Вселенной p = C/T, не имеющее размерности, должно вытекать из некой финалистской теории эволюции.

Согласно нашей теории С = kK 2τ, возраст Вселенной T ≈ Tu = 2 13N 4τ = 2 13N 4C/kK 2(K = 65536, k = 1,1 – зомби-коэффициент, N 4= 42399 – полное число циклов сети человека, Tu – интервал времени от Большого взрыва до недостижимой космологической сингулярности), следовательно F = C/T ≈ C/Tu = kK 2/(2 13N 4) = 13,6 (доверительный интервал обозначить затруднительно из-за неопределенности в значении зомби-коэффициента). Что полностью соответствует астрофизическим и демографическим данным: F = (188 ± 14)/13,8 = 13,6 ± 1.

Таким образом, теория роста сети четвертого ранга позволяет вычислить возраст Вселенной с помощью постоянной Форстера: T = C/F =13,8 ± 1 млрд лет. Однако высокой точности ожидать здесь не следует: дело в том, что точность, с которой может быть определена постоянная C ограничена по принципиальным соображениям.

Если принять, что С = 189 ± 1,3 млрд, что представляется, по нашему мнению, наиболее правдоподобным (см. далее), то эта точность возрастает на порядок: T =13,9 ± 0,1 млрд лет. Теория роста сети пятого ранга, как мы это покажем в дальнейшем, позволяет вычислить возраст Вселенной с точностью до пяти значащих цифр: T =13,8050 ± 0,0002 млрд лет.

С другой стороны, зная возраст Вселенной можно найти постоянную Форстера: C = FT = 188 млрд лет, и гипербола роста населения Земли может быть определена с точностью до начального условия. (Важным отличием нашей модели от всех прочих является то, что постоянную Форстера можно вывести из космологических данных.) В качестве начального условия выберем значение численности в тот момент времени t c, когда сеть становится совершенной: N(t c) = k*K 2= 1,1*2 32= 4,72 млрд; в этот момент, согласно теории, до сингулярности остается всего лишь шаг исторического времени.

По демографическим данным, довольно точным для второй половины XX столетия, находим, что t c= 1982 г. Теперь можно найти точку сингулярности теоретической гиперболы: t 0= 1982 +188 /4,72 = 2022 г. Поскольку гиперболическое уравнение N = C/(t 0– t), постоянная Форстера C и точка сингулярности t 0были выведены на основе теории роста сети четвертого ранга – эмпирический закон гиперболического роста населения Земли, открытый Форстером, получен нами теоретически.